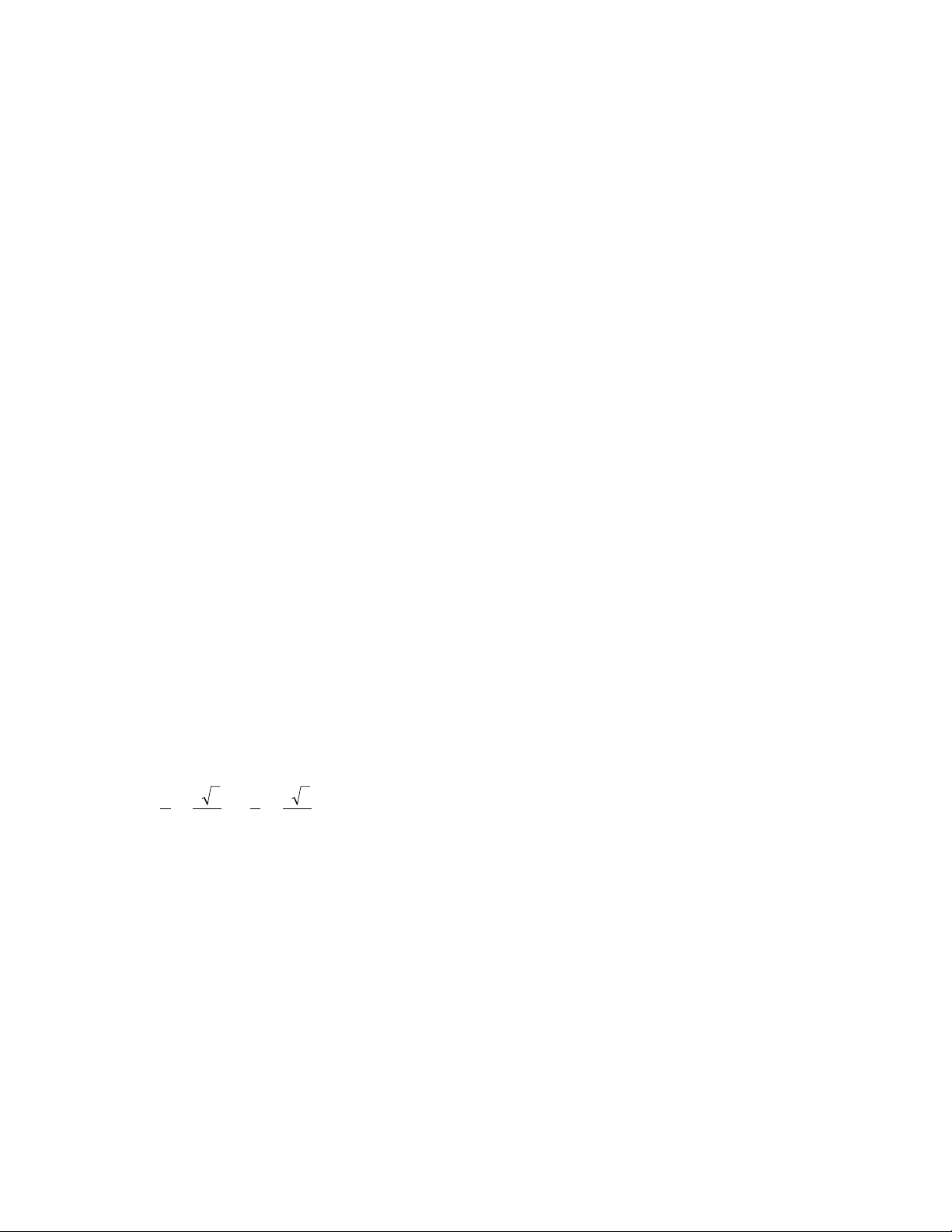


112 cube root/nth root

“stack” pieces of the cube during the slicing process so

as to cut through several pieces at once. (To see this,

consider the innermost cube among the 27 little cubes.

It has six planar faces, each of which need to be cut. As

no single planar cut will slice two of those faces, a min-

imum of six cuts is indeed required to form the 27 little

cubes.) It is possible, however, to dice a large cube into

4 ×4 ×4 = 64 smaller cubes in fewer than nine slices if

“stacking” is permitted (six will suffice). Nine slices

suffice to dice a cube into 5 ×5 ×5 = 125 smaller

cubes. In general, the minimum number of slices

required to subdivide a large cube into n×n×n= n3

smaller cubes is given by the formula:

3 log2n

making use of the

CEILING FUNCTION

.

The four-dimensional analog of a cube is a

HYPERCUBE

.

See also

FLOOR

/

CEILING

/

FRACTIONAL PART FUNC

-

TIONS

;

DUPLICATING THE CUBE

;

PARALLELEPIPED

;

PRISM

.

cube root/nth root The cube root of a number ais a

value xsuch that x3= a. We write 3

√

–

afor the cube root

of a.

Every real number ahas exactly one real cube root.

For instance, the cube root of 27 is 3 (since 3 ×3 ×3

equals 27), and the cube root of –8 is –2 (since –2 ×–2

×–2 equals –8). If one works within the realm of com-

plex numbers, then the

FUNDAMENTAL THEOREM OF

ALGEBRA

shows that every number has exactly three

complex cube roots. For instance, the three cube roots

of 27 are , and 3. A study of

the nth roots of unity shows that the three complex

cube roots of a number lie on the vertices of an equilat-

eral triangle in the complex plane.

In general, the nth root of a number ais a value x

such that xn= a. Again, the fundamental theorem of

algebra shows that every number has exactly ncom-

plex nth roots. If ais a real number, then ahas a real

nth root if ais positive. (For example, a fourth root of

16 is 2.) If ais a negative real number, then a real nth

root exists only if nis odd. (For example, –243 has a

fifth root, namely –3, but no real fourth root.) The real

nth root of a number a, if it exists, is denoted n

√

–

a.

See also

CUBIC EQUATION

;

ROOT

;

SQUARE ROOT

.

cubic equation Any degree-three

POLYNOMIAL

equa-

tion of the form ax3+ bx2+ cx + d= 0 with a≠0 is

called a cubic equation.

During the Renaissance, scholars sought for a gen-

eral arithmetic formula in terms of the coefficients a, b,

c, and dthat would solve all cubic equations (one akin

to the famous

QUADRATIC

formula for solving degree-

two equations). At the time, however, scholars were not

comfortable working with

NEGATIVE NUMBERS

, or with

ZERO

as a number, and wrote equations in a form that

avoided their appearance. (For instance, the cubic x3–

2x+ 5 = 0 was cast as x3+ 5 = 2x.) Mathematicians

consequently thought that there were eight different

types of cubic equations to solve.

Italian scholar S

CIPIONE DEL

F

ERRO

(1465–1526)

was the first to make progress in solving certain cubics,

but never published his results. Later, the scholar N

IC

-

COLÒ

T

ARTAGLIA

(ca. 1499–1557) succeeded in solving

some additional classes of cubics. G

IROLAMO

C

AR

-

DANO

(1501–76) published Tartaglia’s work (without

Tartaglia’s consent) in his epic 1545 piece Ars magna

(The great art) and developed a general approach that

solves all cubic equations. The formula he devised is

today called “Cardano’s formula” or the “Cardano-

Tartaglia formula.” We describe it here using modern

notation:

By dividing the cubic equation through by the lead-

ing coefficient a, we can assume that we are working

with a cubic of the form:

x3+ Bx2+ Cx + D= 0

for numbers , , and . Substituting

simplifies the equation further to one without

a square term:

y3+ py + q= 0

(Here and .) This form

of the cubic is called the reduced cubic, and any solu-

tion yto this equation corresponds to a solution

of the original equation.

Assume that the equation has a solution that can

be written as the sum of two quantities: y= u+ v. Sub-

stituting these variables yields:

b

x = y –

—

3a

2B3BC

q=

—

–

—

+ D

27 3

B2

p = C –

—

3

B

x = y –

—

3

d

D=

—

a

c

C=

—

a

b

B=

—

a