f(x + h) – f(x)

––——

—

h

f(t + h) – f(t)

––——

—

h

f(x + h) – f(x)

––——

—

h

dy

––

dx

132 differential calculus

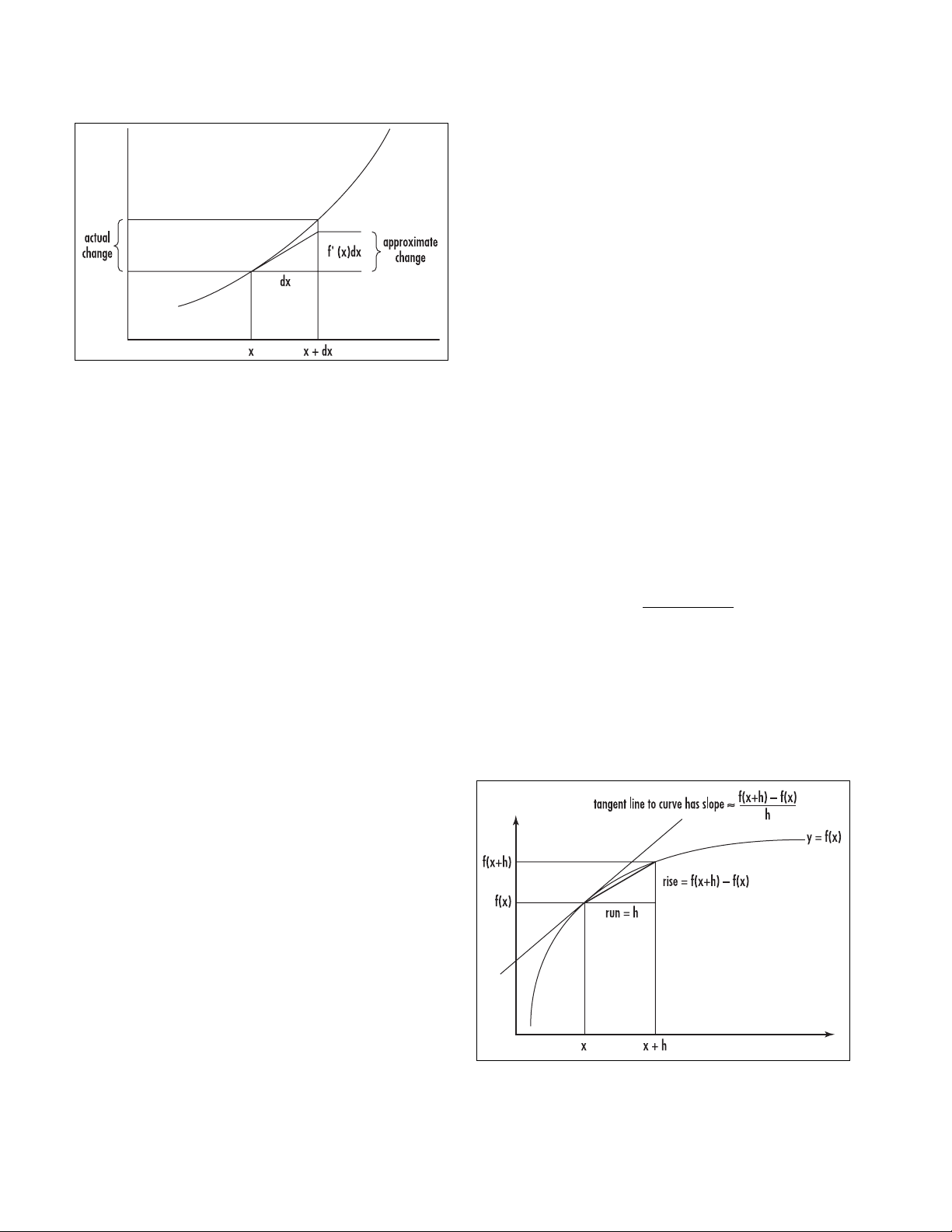
The differential

Computing the derivative

small straight-line segment tangent to the graph at x.

The slope of this tangent line is the

DERIVATIVE

f′(x).

Using the symbol dx to represent a small change in the

x-variable, we see that the corresponding change in the

y-variable is approximately dy = f′(x)dx. The quantities

dx and dy are called differentials.

G

OTTFRIED

W

ILHELM

L

EIBNIZ

(1646–1716) based

his development of the theory of

CALCULUS

on the idea

of a differential. Today we use the notation for the

derivative f′(x),deliberately suggestive of Leibniz’s ideas.

See also

HISTORY OF CALCULUS

(essay);

NUMERICAL

DIFFERENTIATION

.

differential calculus This branch of

CALCULUS

deals

with notions of

SLOPE

, rates of change and ratios of

change. For example, a study of

VELOCITY

, which can

be described as the rate of change of position, falls

under the study of differential calculus, as do other

concepts that arise in the study of motion.

If a quantity yis a

FUNCTION

of another quantity

x, y = f(x) say, then each change in the x-variable,

x→x+h, produces a corresponding change in the

y-variable: f(x)→f(x + h). The ratio of the changes of

the two variables is: . Graphically, this

represents the slope (the “rise” over the “run”) of the

line segment connecting the two points (x,f(x)) and

(x+h,f(x+h)) on the graph of the curve y=f(x).

The slope of this line segment, for a fixed change h

in the x-variable, depends on the shape of the curve

and will typically change from point to point. A very

steep curve will give a large rise for a fixed run, for

example, whereas a curve that rises slowly will give a

low value for slope. In all cases, if the value his very

small, then the slope of the line segment described

above approximates the slope of the

TANGENT

line to

the curve at position x. The smaller the value of h, the

better is the approximation.

In another setting, if y = f(t) represents the position

of a car along a highway at time t, then, over hseconds

of travel, the automobile changes position by amount

f(t+ h) – f(t),and the ratio represents

the average rate of change of position, or the average

velocity, of the car over hseconds of travel. If the value h

is small, then this quantity approximates the actual speed

of the car at time tas read by the speedometer. The

smaller the value of h, the better is the approximation.

The ratio is called a “Newton

quotient” to honor the work of S

IR

I

SAAC

N

EWTON

(1642–1727) in the discovery and development of cal-

culus, and the

LIMIT

,

if it exists, is called the derivative of the function f(x).It

represents the slope of the (tangent line to the) graph

y=f(x) at position x, or, alternatively, the instantaneous

rate of change of the variable y = f(x) at position/time x.