distance formula 141

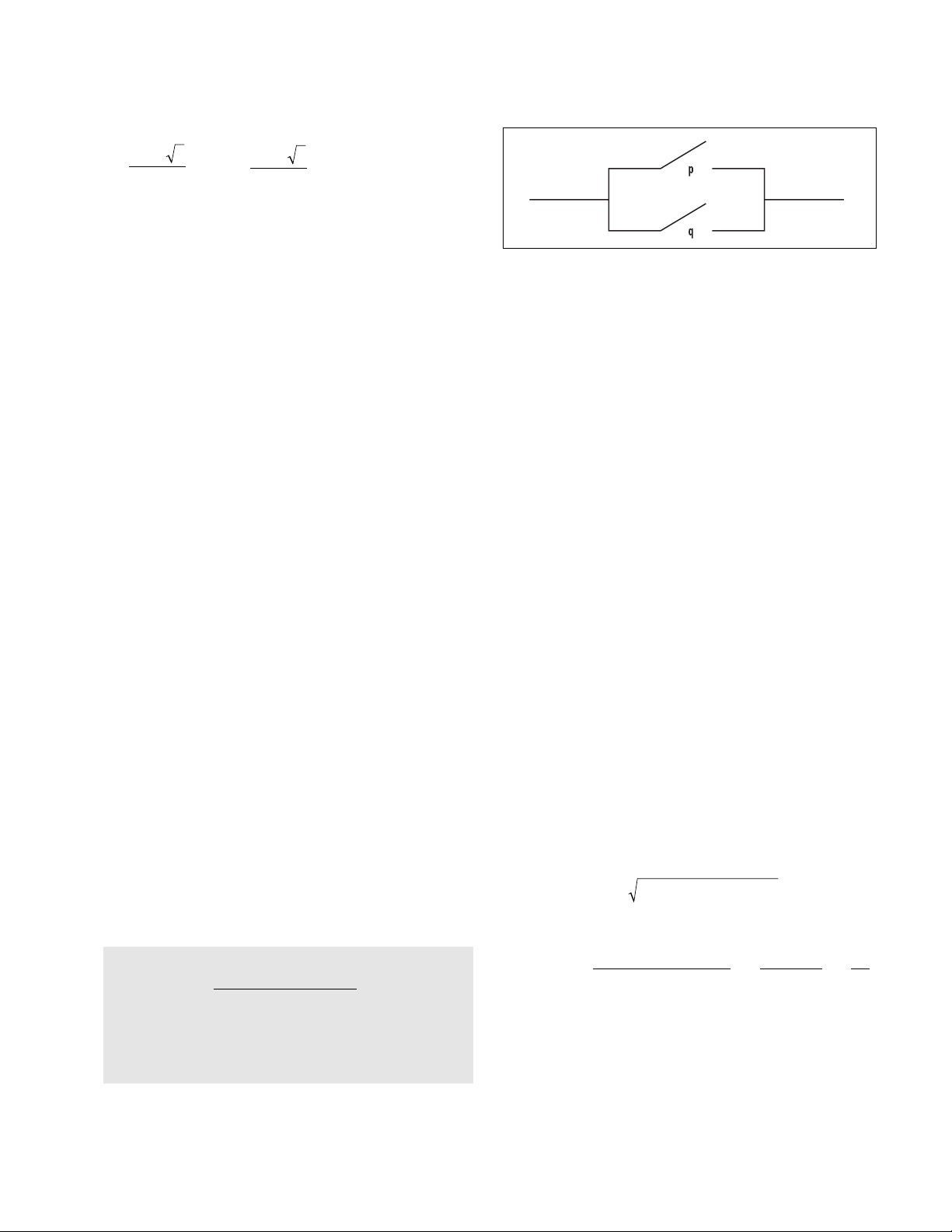
Disjunction circuit

pqp

∨q

TTT

TFT

FTT

FFF

x2+ x+ 1 = 0, with discriminant –3, has solutions

and .

More generally, the discriminant of any

POLYNO

-

MIAL

equation is defined to be the product of the differ-

ences squared of all the possible pairs of roots of the

equation. For example, if a

CUBIC EQUATION

has three

roots r1, r2, and r3(possibly repeated), then the dis-

criminant of cubic is the product:

(r1– r2)2(r2– r3)2(r3– r1)2

It is possible to find a formula for the discriminant in

terms of the coefficients appearing in the equation. For

the case of a quadratic, it turns out to be precisely the

quantity b2–4ac described above.

disjunction (“or” statement) A compound statement

of the form “por q” is known as a disjunction. For

example, “I visited Sydney or Melbourne” is an exam-

ple of a disjunction.

Disjunctions can be interpreted in one of two ways.

If a disjunction “por q” is read as

por q, but not both

(“I visited just one of the two cities”), then it is said to

be “exclusive,” and the disjunction is called an “exclu-

sive or” (sometimes denoted XOR). Interpreted as

por q, or possibly both

(“I visited at least one of the cities”), then the disjunc-

tion is said to be “inclusive” and is called an “inclusive

or.” In

FORMAL LOGIC

(and in most of mathematics),

disjunctions are always used in the inclusive sense. It is

denoted in symbols by p∨qand has the following

TRUTH TABLE

:

A disjunction can be modeled via a parallel circuit.

If T denotes the flow of current, then current moves

through the circuit as a whole precisely when one, or

both, switches pand qadmit current flow.

See also

CONJUNCTION

.

displacement The distance traveled by a moving

object is sometimes called its displacement. Physicists

often use the symbol sto denote displacement. The rate

of change of displacement is called

VELOCITY

.

See also

DIFFERENTIAL CALCULUS

.

distance formula The distance dbetween two given

points P1= (x1,y1) and P2= (x2,y2) in the plane is the

length of the line segment that connects P1to P2. If one

regards this line segment as the hypotenuse of a right

triangle with one leg horizontal, that is, parallel to the

x-axis, and one leg vertical, parallel to the y-axis, then

P

YTHAGORAS

’

S THEOREM

can be employed to find a

formula for d. The length of the horizontal leg is the

difference of the x-coordinates x2– x1or x1– x2,

whichever is positive, and the length of the vertical leg

is the difference of the y-coordinates, y2– y1or y1– y2.

Thus, by Pythagoras’s result, we have:

This is called the two-dimensional distance formula.

For example, the distance between the points (–3,5)

and (2,1) is = = .

Notice that, as one would expect, the distance formula

is symmetric in the sense that the distance between P1

and P2is the same as the distance between P2and P1.

The set of all points (x,y) in the plane a fixed distance r

from a given point C= (a,b) form a

CIRCLE

with radius

√41√52+ (–4)2

√(2 – (–3))2+ (1 – 5)2