3x2– 5

———

1 + x4

even and odd numbers 177

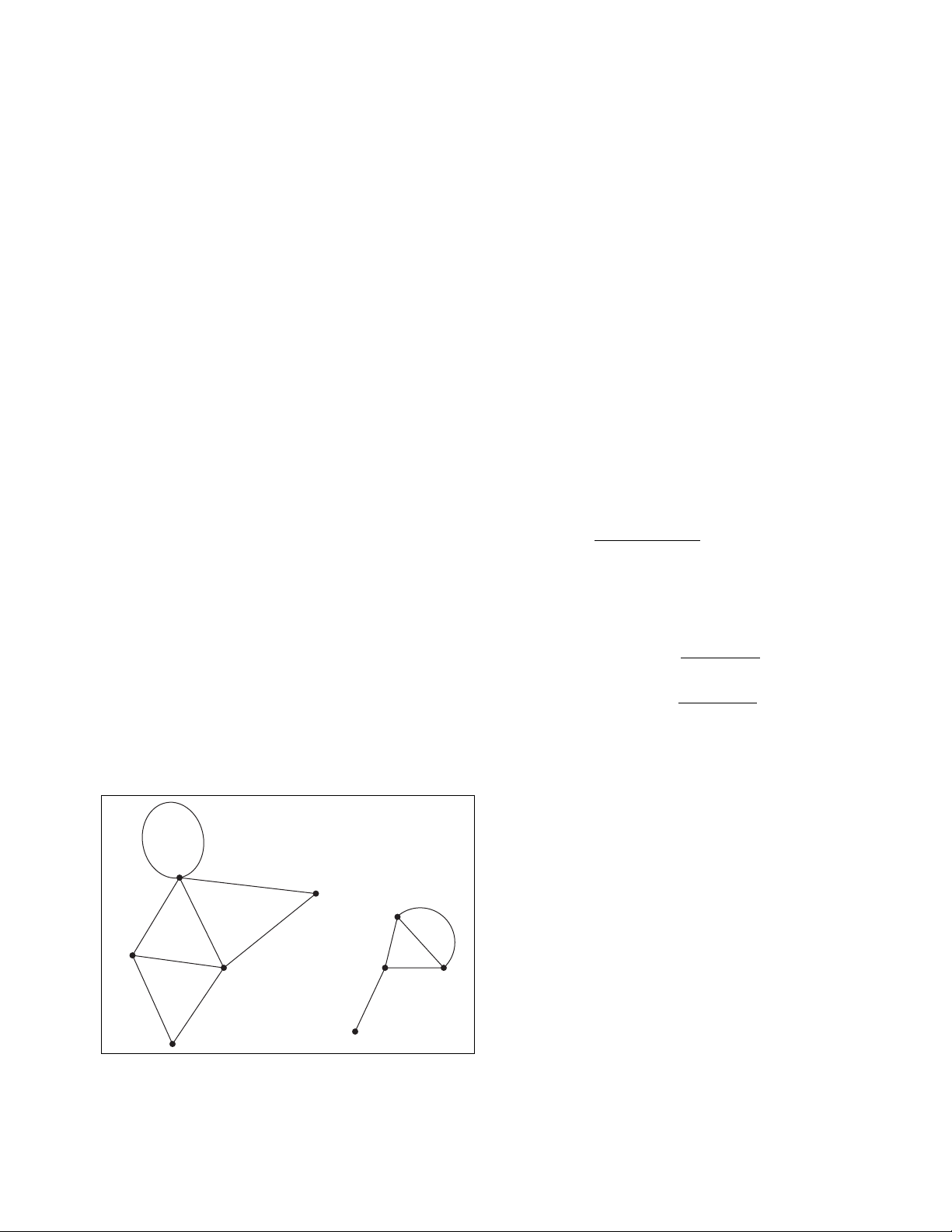
A graph with two components

decreasing the value of cby 1). In all cases the formula

v– e+ r= 1 + cremains balanced.

The formula is usually applied to a graph that is

connected, that is, has only one component (c= 1). In

this case the formula reads:

v– e+ r= 2

and this version of the equation is usually called Euler’s

theorem.

The vertices, edges, and faces of a

POLYHEDRON

can

be thought of as a connected graph. For example, a

cube with its top face removed and pushed flat onto a

plane yields a graph with eight vertices and 12 edges

dividing the plane into six regions. (The large “outer”

region corresponds to the top face of the cube that was

removed.) We still have: v– e+ r= 2. In general, for any

polyhedron with vvertices, eedges, and ffaces we have:

v– e+ f= 2

This was first observed by R

ENÉ

D

ESCARTES

in 1635.

Euler had no knowledge of Descartes’s work when he

developed the formula in the more general setting of

graph theory. For this reason, this famous formula is

also called the Euler-Descartes formula.

This result holds true only for graphs that lie on

the plane (or polyhedra that can be pushed flat onto a

plane). One can show that for connected graphs drawn

on a

TORUS

, for example, the formula must be adjusted

to read: v– e+ r= 0. For example, if a polyhedron

contains a hole (say, a cube with a square hole drilled

through it), one has: v– e+ f= 0. (There is one techni-

cal difficulty here: one needs to be sure that each region

or face under consideration is not itself an

ANNULUS

.

One may need to draw in extra edges to break regions

into suitable form.)

even and odd functions A function y= f(x) is said

to be even if, for each x, the function takes the same

value at both xand –x, that is, f(–x) = f(x) for all val-

ues of x. The graph of an even function is consequently

symmetrical about the vertical axis. The functions x2,

cos(x),and , for example, are even functions.

A function y= f(x) is said to be odd if, for each x,

the function takes opposite values at xand –x, that is,

f(–x) = –f(x) for all values of x. The graph of an odd

function is consequently symmetric with respect to a

180°rotation about the origin. The functions x, x3,

sin(x),and ,for example, are odd

functions.

Any function g(x) can be expressed as the sum of

an even and an odd function. Let:

Then feven(x) is even, fodd(x) is odd, and g(x) = feven(x) +

fodd(x).

The F

OURIER SERIES

of any even function contains

only cosine terms, and the Fourier series of any odd

function only sine terms. The absolute value of any odd

function f(x) is an even function, that is, if y= |f(x)|,

then yis even.

even and odd numbers Working solely in the realm

of the whole numbers, a number is said to be even if it

is divisible by 2, and odd if it leaves a remainder of 1

when divided by 2. For example 18 is divisible by 2 and

so is even, and 23 leaves a remainder of 1 and so is odd.

There is a physical interpretation to the evenness or

oddness of a number: An even number of pebbles, say,

represents a pile that can be split into two equal