graph 233

A typical graph

gradient The

SLOPE

of a line is sometimes called its

gradient or grade. For example, the gradient of the line

connecting the two points A= (a1,a2) and B= (b1,b2),

denoted mAB, is given by:

Three points A, B, and Cin the plane are

COLLINEAR

if

the gradients mAB and mAC are equal.

In the setting of multivariable calculus—the study

of

CALCULUS

applied to

FUNCTIONS

of more than one

variable—the gradient of a function f(x,y,z) of three

VARIABLES

, also called the “grad of f,” is defined to be

the

VECTOR

of its

PARTIAL DERIVATIVE

s. It is denoted

grad(f) or fand is given by:

Such a quantity proves to be useful in computing the

DIRECTIONAL DERIVATIVE

of a function. In physics, f

is also used to describe the spatial variation in the mag-

nitude of a force, such as a gravitational force or a

magnetic force. The study of directional derivatives

shows that the quantity fcalculated at a point repre-

sents the direction from that point in which the rate of

change of the force fis a maximum.

See also

DIV

.

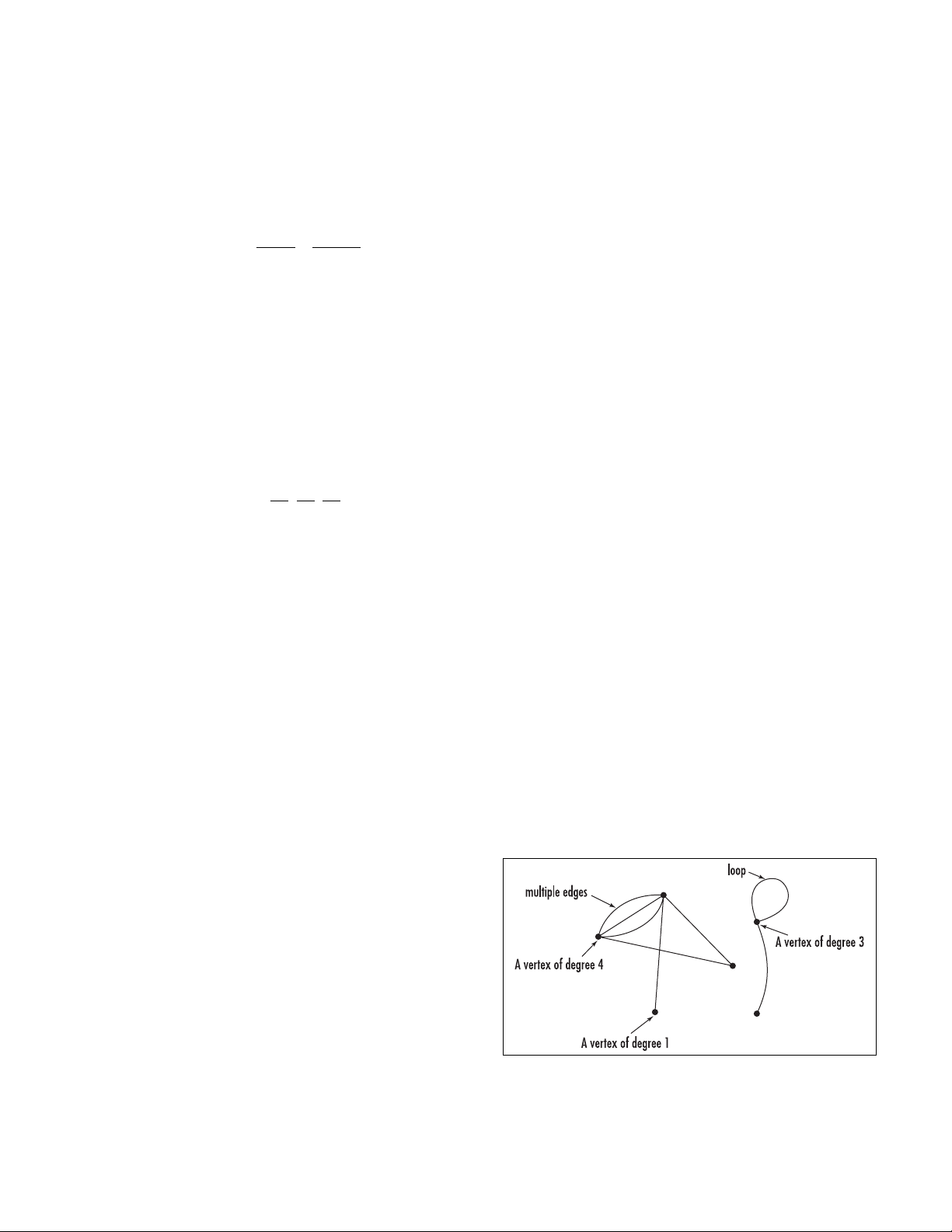
graph (network) Any diagram of points and line seg-

ments connecting pairs of points is called a graph. The

points are usually called vertices or nodes, and the line

segments are called edges. More than one edge is

allowed to connect the same pair of vertices to yield a set

of multiple edges. One can also permit an edge connect-

ing a vertex to itself via a loop. Edges can intersect, but

the places where they cross are not considered vertices.

For example, the following picture is a graph. It has just

six vertices and comes in two disconnected pieces.

A graph that comes in just one piece is called con-

nected. This means that it is always possible to travel

from any one vertex to any other by traversing a

sequence of edges.

Graphs can be used to codify information. For

example, a graph might represent the network of possi-

ble flight routes between cities, the flow of information

between departments in a large organization, or even

the set of acquaintances among people attending a

party. (Each vertex represents a person in the room,

and an edge is drawn between two vertices if the corre-

sponding two people know each other.) The general

study of graphs can translate into interesting facts

about travel possibilities, streamlining data flow,

acquaintanceships, and the like.

The degree (or valence) of a vertex is the number of

edges that meet at that vertex. Loops are counted twice.

A graph is called complete if every vertex is con-

nected to each and every other vertex by a single edge.

For example, the complete graph on four vertices looks

like a square with the two diagonals drawn in. Each

vertex has degree three.

A graph is called planar if it can be drawn on a

plane without two edges crossing. The complete graph

on four vertices is planar if one draws one of the diago-

nals “outside the square.” The

THREE

-

UTILITIES PROB

-

LEM

is an example of a graph that is not planar.

A cycle in a graph is a sequence of edges that starts

and ends at the same vertex and does not travel over

the same edge twice. Finding an “Euler circuit,” i.e., is,

a cycle that traverses each and every edge in a graph

precisely once, is an old problem. (See

GRAPH THEORY

.)

A connected graph containing no loops or cycles is

called a tree. These graphs look like a series of forking

branches, and hence the name tree. Any tree diagram,

such as a

PROBABILITY

, tree is an example of a graph

that is a tree. It follows from E

ULER

’

S THEOREM

that

any connected graph with nvertices and n–1 edges

must be a tree.

See also

CRITICAL PATH

; E

ULERIAN PATH

/

CIRCUIT

;

H

AMILTONIAN PATH

/

CIRCUIT

;

TOURNAMENT

.