hyperbola 253

Hyperbola

him in writing his 11-part commentary on the mathe-

matical work of C

LAUDIUS

P

TOLEMY

(85–165

C

.

E

.) and

on his production of a revised version of E

UCLID

’s The

Elements. Hypatia produced her own commentaries on

classical pieces, including Diophantus’s famous Arith-

metica, Apollonius’s Conics, and astronomical works

by Ptolemy. All of her work, however, is today lost, and

we know of them only through references made by

later scholars.

Around 400

C

.

E

. Hypatia headed the Platonist

school at Alexandria, where she consulted on scientific

matters and lectured on philosophy and mathematics.

During this time, Christianity surfaced as the dominant

religion of the region, and fanatics felt threatened by

her intellect and scholarship. Around 415

C

.

E

. Hypatia

was brutally murdered by a group of religious follow-

ers who deemed her philosophical views pagan. Many

historians suggest that the death of Hypatia marks the

beginning of Alexandria’s decline as the great center of

scholarship and learning of antiquity.

It is worth mentioning that at least one other

woman is known to have played an active role in

mathematics during the Greek times. In his work Col-

lection, P

APPUS OF

A

LEXANDRIA

(300–350

C

.

E

.) gives

acknowledgment to a female scholar by the name of

Pandrosion. Essentially nothing is known about her.

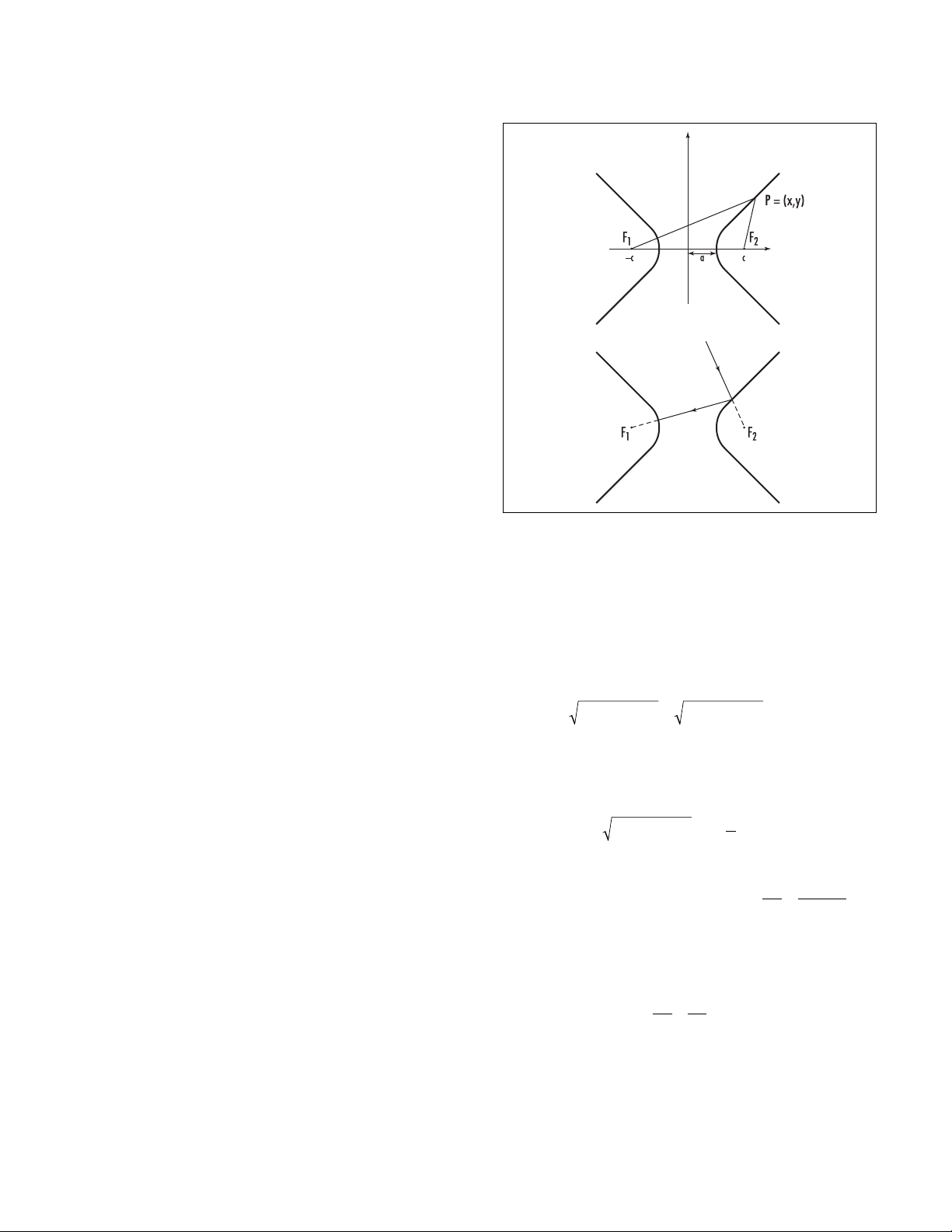
hyperbola As one of the

CONIC SECTIONS

, the hyper-

bola is the plane curve consisting of all points Pwhose

distances from two given points F1and F2in the plane

have a constant difference. The two fixed points F1

and F2are called the foci of the hyperbola. The hyper-

bola also arises as the curve produced by the intersec-

tion of a plane with the two nappes of a right circular

CONE

.

Using the notation |PF1| and |PF2| for the lengths of

the line segments connecting Pto F1and F2, respec-

tively, the defining condition of a hyperbola can be

written as one of two equations:

|PF1| – |PF2| = dor |PF2| – |PF1| = d

where ddenotes the constant difference. Each equation

defines its own curve, or branch, of the same hyperbola.

The equation of a hyperbola can be found by intro-

ducing a coordinate system in which the foci are

located at positions F1= (–c, 0) and F2= (c,0), for some

positive number c. It is convenient to write d= 2a, for

some a> 0. If P= (x,y) is an arbitrary point on the

hyperbola, then, according to the

DISTANCE FORMULA

,

the defining conditions read:

Moving the second radical to the right-hand side,

squaring, and simplifying yields the equation:

Squaring and simplifying again yields .

Noting that cis greater than a, we can set the positive

quantity c2– a2as equal to b2, for some b> 0. Thus the

equation of the hyperbola is:

Conversely, one can show that any equation of this form

does indeed yield a hyperbola with foci at positions