b

–

a

√a2+ b2

254 hyperbolic functions

The trigonometric and the hyperbolic functions

a

a

–

e

(±,0), and whose points Phave distances with

common difference 2afrom the foci. This equation

also reveals that the hyperbola has slant

ASYMPTOTE

s

y=± x.

Hyperbolas have the following reflection property:

any ray of light that approaches the convex side of one

branch along a line pointing toward one focus is

reflected directly toward the other focus. (This property

can be proved in a similar way that the reflection prop-

erty of a

PARABOLA

is proved.)

Hyperbolas appear in the folding of a thin piece of

paper. Draw a circle and a dot outside the circle on a

sheet of paper. Fold the dot onto the circle and crease

the paper. Open up the fold and do this again, this time

folding the dot to a different point on the circle. As you

do this many times, one branch of a hyperbola will

emerge along the side of all the creases. The marked

dot is one focus of the hyperbola, and the center of the

circle is the other. The radius of the circle is the con-

stant difference of distances of a point on the hyper-

bola from the two foci.

In the process of deriving the equation of a hyper-

bola, we presented the equation:

valid for one branch of the figure at least. Set

. This is called the

ECCENTRICITY

of the hyperbola and has a value greater than 1. The

above equation can be rewritten:

The numerator of the quantity on the left side is the

distance of a given point Pfrom a focus, and the

denominator is the distance of the point Pfrom the ver-

tical line x= , called a directrix of the hyperbola.

This formulation provides an alternative characteriza-

tion of the hyperbola:

A hyperbola is the set of all points Psuch that

the ratio of its distance from a fixed point (the

focus) to its distance from a fixed line (the

directrix) equals a constant e> 1.

See also A

POLLONIUS

’

S CIRCLE

;

ELLIPSE

.

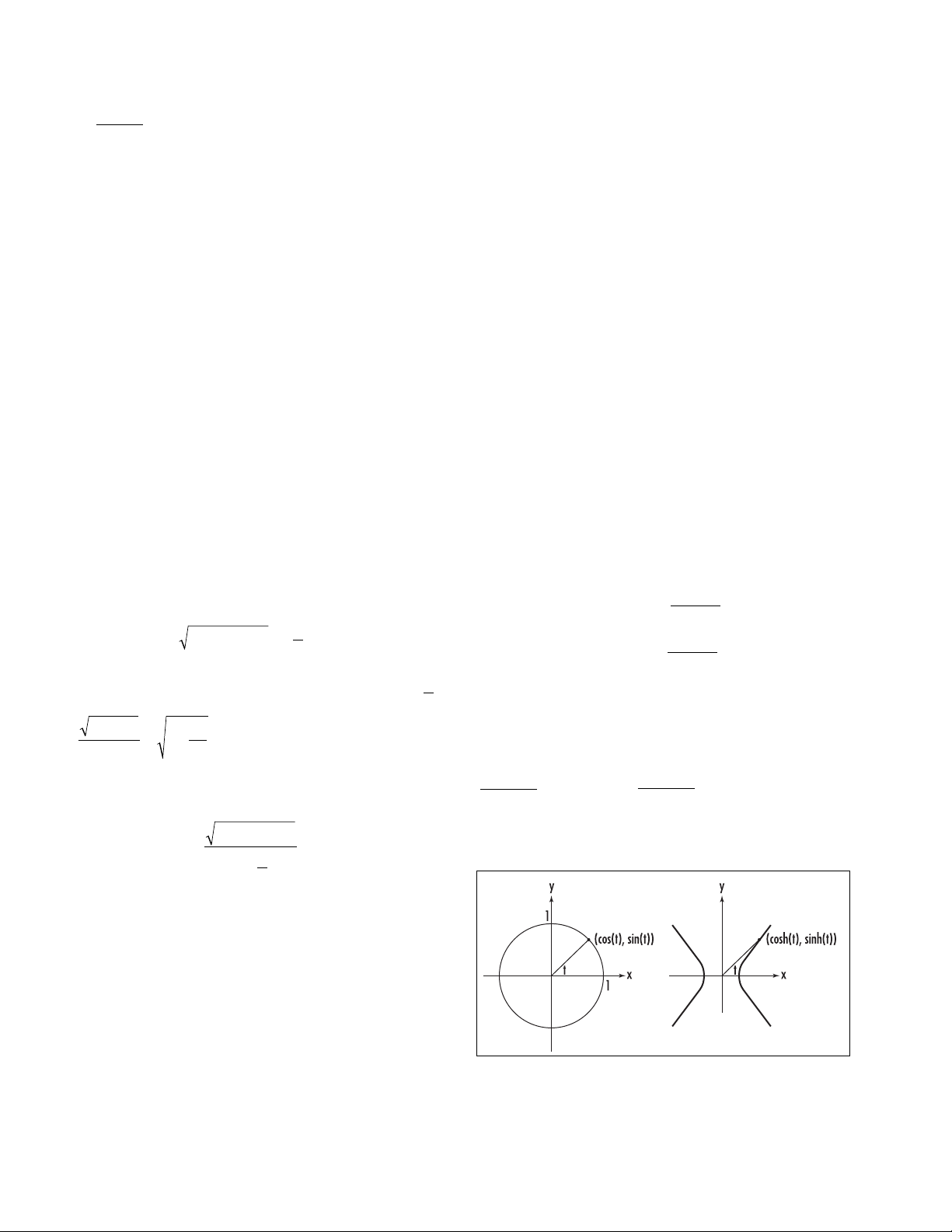
hyperbolic functions In analogy to the fact that the

sine and cosine functions of

TRIGONOMETRY

represent

the coordinates of a point on the unit circle, x2+ y2= 1,

the hyperbolic functions represent the coordinates of a

point on the right branch of a

HYPERBOLA

, x2– y2= 1.

Specifically, the x-coordinate of a point on the

curve, at an “angle” t, is called the hyperbolic cosine

function, and is denoted cosh(t),and the y-coordinate

is called the hyperbolic sine function, denoted sinh(t).

We have:

cosh2(t) – sinh2(t) = 1

One can also see that cosh(–t) = cosh(t) and sinh(–t) =

–sinh(t).

Mathematicians sometimes define the hyperbolic

sine and cosine functions via the formulae:

One can check that these formulae do indeed satisfy the

equation of a hyperbola x2– y2= 1 with x> 0, and so

must indeed be the coordinates of its points. (These

equations are reminiscent of the formula

and , which follow from

E

ULER

’

S FORMULA

for ordinary trigonometric functions.)