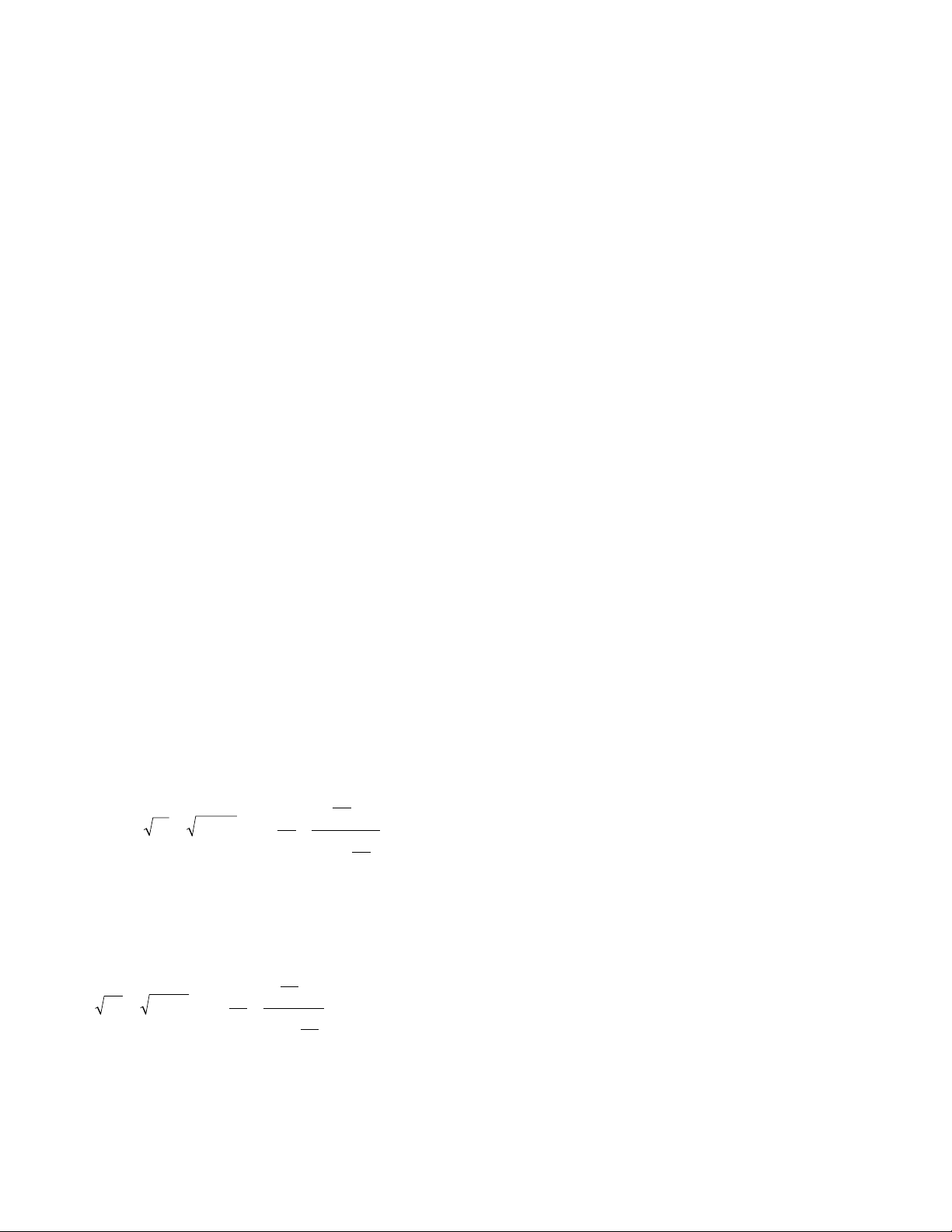
264 Indian mathematics

The earliest written records of Indian culture are

the religious texts the Vedas, dating between 1500

B

.

C

.

E

. and 800

B

.

C

.

E

. Although not mathematical in

content, appendices to the texts give specific rules for

constructing altars, exhibiting a thorough understand-

ing of the basic principles of geometry. Early versions

of the digits 0 through 9 were used at this time.

By 600

C

.

E

., the Vedic religion had gone into

decline, and Jainism came to the fore. During this

period mathematics was driven by the needs of the

religion and its demands for careful astronomical

observations to pinpoint the exact times of religious

observances and the development of an accurate cal-

endar. The decimal representation system was now

fully developed, and scholars were able to make pre-

cise and surprisingly accurate calculations. The math-

ematician A

–

RYABHATA

(ca. 500

C

.

E

.), for instance, had

developed a theory of

TRIGONOMETRY

to aid astro-

nomical calculations, had developed methods for

extracting square roots, evaluated πto a high degree

of accuracy, and was able to find integer solutions to

a large class of equations that arose from astronomi-

cal theories.

One written text from this period was discovered

in 1881 in the town of Bakhshali, now in Pakistan.

Written on birch bark, the Bakhshali manuscript shows

that mathematicians were also comfortable with frac-

tions, basic algebraic manipulations (they used a dot to

represent an unknown quantity), and sophisticated

approximation formulae. For example, the manuscript

describes, in words, the following approximation for

the square root of a number N:

Here a2is the largest perfect square smaller than Nand

b= N– a2. For example, we have:

which is correct to seven decimal places.

Two mathematical research centers were formed in

India during the era of Jainism, both astronomical

observatories. A

–ryabhata headed the first center at

Kusumapura in the northeast of the Indian subconti-

nent, and mathematician Varahamihira, who also made

contributions to astronomy and trigonometry, headed

the second center at Ujjain, also in the north.

Varahamihira was succeeded by the seventh-cen-

tury mathematician B

RAHMAGUPTA

, who, in his famous

work Brahmasphutasiddhanta (The opening of the uni-

verse), introduced and explained the arithmetic of non-

positive numbers. He was the first mathematician in

history to give zero the status of a number, defining it

to be the result of subtracting a quantity from itself.

Brahmagupta’s work also includes a formula for the

area of a cyclic quadrilateral in terms of its sides (today

called B

RAHMAGUPTA

’

S FORMULA

), and presents meth-

ods for solving linear and quadratic equations, as well

as systems of equations. Brahmagupta also developed

sophisticated interpolation techniques for computing

sine values in trigonometry.

For the next 200 years, Indian scholars worked

to refine further methods of trigonometry and tech-

niques of astronomical calculation. The mathemati-

cian B

H

–

ASKARA

II of the 12th century made advances

in number theory, algebra, combinatorics, and astron-

omy, and wrote a comprehensive text summarizing

the state of mathematics and astronomy in India at his

time. Soon afterward, other Indian scholars developed

these ideas further. Jaina mathematicians also clarified

the standard

EXPONENT

rules and manipulated expo-

nents in a manner that suggests today that they were

also familiar with the basic principles of

LOGARITHM

s.

The 14th-century scholar M

ADHAVA OF

S

ANGAMA

-

GRAMMA

made significant advances in

ANALYSIS

. He

produced the infinite series expansions of trigonometric

and inverse trigonometric functions (today called T

AY

-

LOR SERIES

), discovered the

BINOMIAL THEOREM

, and

even produced G

REGORY

’

S SERIES

for π, which he used to

approximate its value to a considerably accurate degree.

During the first millennium India had very little

contact with the cultures of the West. News of the deci-

mal representation system, however, did manage to

spread to other countries relatively quickly. A

manuscript written in Syria in 662 discusses the new

method of calculation, and there is evidence that the

decimal system was being used in Cambodia and other

Asian countries soon afterward. By the ninth century,