the material, without ever cheating by crossing over the
edge of the hole given by the waist band.
If one cuts a pair of trousers sewn to make a (punc-
tured) Klein bottle in half along the line that follows the
inner and outer seams of the trousers, then the model
falls into two pieces, each of which is easily seen to have
arisen from a Möbius band. This shows that a Klein bot-
tle can also be thought of as the union of two Möbius
bands adjoined along their edges. (If one physically
attempts to sew together two Möbius bands, one soon
finds it is necessary to puncture a band to produce a hole
akin to the hole for the waist of a pair of trousers.)
Klein-four group (viergruppe) There are essentially
only two
GROUP
s with just four elements. The first is
the “cyclic group” C4given by the rotational symme-
tries of a square, C4= {1, R, R2, R3}, where Rrepre-
sents a 90°rotation of a square in a clockwise direction
and 1 is the
IDENTITY ELEMENT
, a rotation of zero
degrees. As a rotation of 360°is equivalent to no
action, we have that R4= 1. Multiplication in this
group is given by the product rule of exponents. We
have, for example, that R2×R3= R5= R.
The second group with just four elements is called
the Klein-four group. Denoting its elements as 1, a, b,
and c, with 1 being the identity element, it has a multi-
plication table given by:
This group can also be represented by a set of symme-
tries of a square. Set ato mean a reflection about a
vertical axis, ba reflection about a horizontal axis,
and ca rotation of 180°. We have, for instance, that a
vertical reflection followed by a rotation of 180°is the
equivalent of a horizontal reflection (c×a= b), and
that two reflections about the same axis lead to the
identity (a×a= b×b= 1).
knot theory The branch of
TOPOLOGY
that studies
the properties of closed loops embedded in three-
dimensional space is called knot theory. Each loop
studied, called a knot, represents the path traced by a
piece of string interlaced in space (without self-intersec-
tion) whose free ends have been joined together. If one
tangled piece of string can be physically transformed
into an exact copy of a second tangled string (or at
least a mirror image of that second tangle), then we say
that the two knots the strings represent are equivalent.
At present, no one knows a general procedure guaran-
teed to determine with relative ease whether or not two
given knots are equivalent.
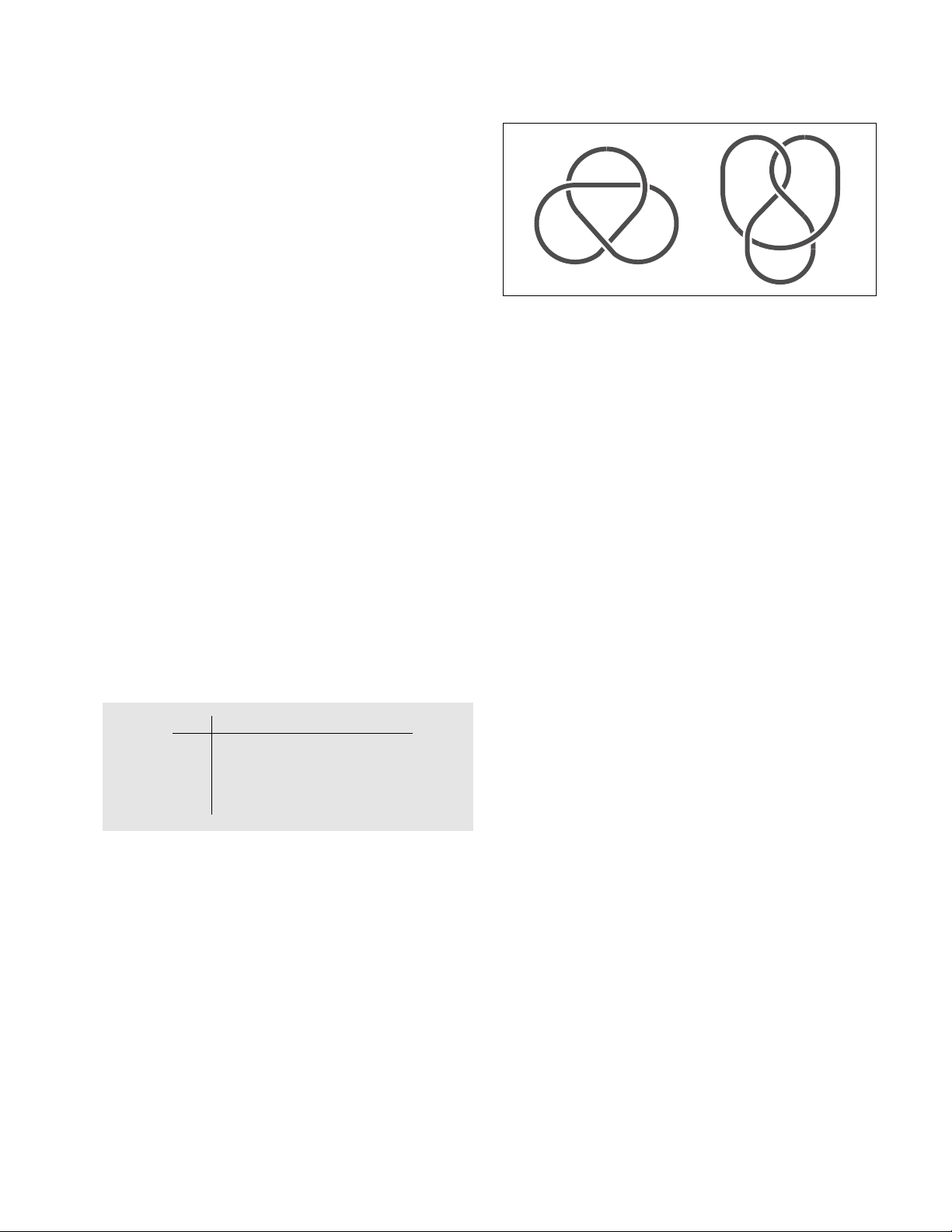
Knots can be depicted on a two-dimensional page
as a picture of a loop that crosses over and under itself.
It is conventional to draw the picture of a given knot
with as few crossings as possible. A picture with just
one or two crossings is equivalent to an untangled loop
(the “unknot”). There is only one knot (up to equiva-
lence) with three crossings and only one with four
crossings. Each are shown above. There are two dis-
tinct knots requiring a minimum of five crossings, three
requiring a minimum of six crossings, and seven requir-
ing a minimum of seven crossings. After this, the num-
ber of distinct knots with a given minimum number of
crossings when drawn on a page grows rapidly.
Knots were first studied by C
ARL
F
RIEDRICH
G
AUSS
(1777–1855) and his student Johann Listing (1808–82).
In 1877 Scottish physicist Peter Tait classified all knots
with up to seven crossings. He also conjectured that no
“alternating knot” (that is, one whose path alternately
crosses over and under itself) is equivalent to the
unknot. A century later, New Zealand mathematician
Vaughn Jones proved him to be correct.
In 1928 American mathematician James Waddell
Alexander discovered a theoretical means to associate to
each knot a
POLYNOMIAL
in such a manner that if two
×1abc
11 abc
aa 1cb
bb c1a
ccba1
knot theory 295
The two knots with fewer than five crossings