law of cosines/law of sines 303

Establishing the law of cosines

Establishing the law of sines

Arrange 16 officers, each from one of four pos-

sible regiments and of one of four possible

ranks, in a 4×4array so that no two officers

in any given row or column come from the

same regiment, nor have the same rank.

Graeco-Latin squares are also sometimes called

Euler squares. Mathematicians have proved that

there is no solution to the officer problem for the

case of 36 officers of six different ranks from six dif-

ferent regiments (nor for the case of four officers

from two regiments of two ranks), but that all other

versions of the officer problem do have solutions. In

other words, n×nGraeco-Latin squares exist for all

values of nexcept n= 2 and n= 6.

Graeco-Latin squares are important in the design

of experiments in scientific studies. For example, if four

species of tomato A, B, C, and D are to be tested with

four different fertilizers α, β, γ, and δ, the plots can be

laid out according to a Graeco-Latin square to be sure

that each species of tomato and each fertilizer appears

in each row and column.

law of averages This “law” refers to the incorrect

belief that previous outcomes of independent runs of a

random trial influence the outcomes of runs yet to

occur. For example, after tossing seven “heads” in a

row, the supposed law of averages would dictate that

“tails” is now a more likely outcome. This of course is

not the case. The chance of tossing tails on the eighth

toss is still 50 percent. The law of averages is a com-

mon misinterpretation of the mathematically correct

LAW OF LARGE NUMBERS

. Gamblers often feel that after

a long string of losses, the chances of winning a next

hand must be considerably greater.

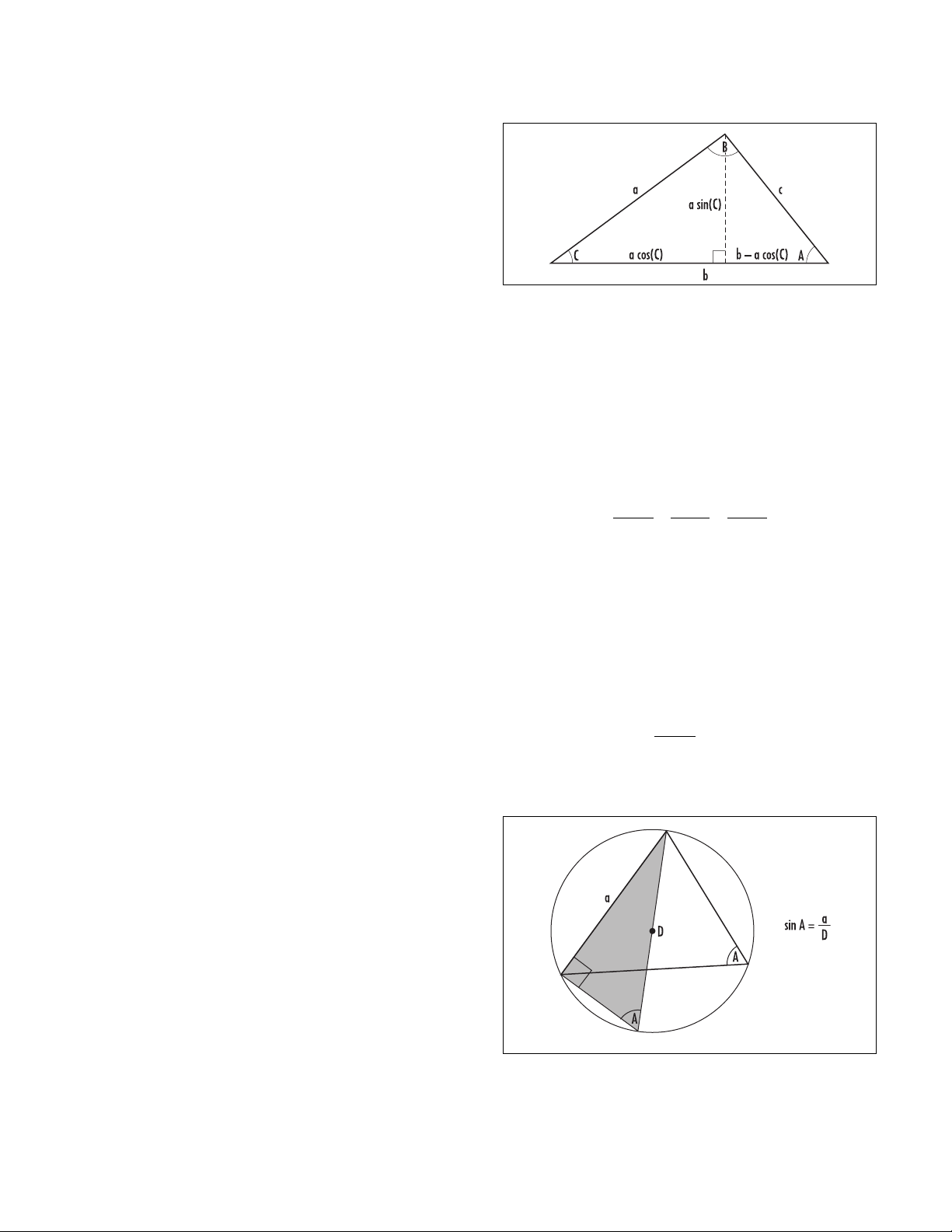
law of cosines/law of sines (cosine rule, sine rule)

Let a,b, and cbe the three side-lengths of a triangle

with interior angles as shown.

The law of cosines asserts:

c2= a2+ b2– 2abcos(C)

(with analogous statements for angles Aand B). When

Cis a right angle, this result reduces to a statement of

P

YTHAGORAS

’

S THEOREM

. Hence the law of cosines can

be regarded as a generalization of this famous result.

The law can be proved by drawing an altitude from the

apex of the triangle and applying Pythagoras’s theorem

to the right-angled triangle containing the altitude and

side cin the picture above.

The law of sines asserts:

This can be proved by drawing the altitudes of the tri-

angle. For example, the altitude above is simultaneously

of length asin(C) and csin(A),thereby establishing part

of the law of sines.

Drawing the

CIRCUMCIRCLE

to the triangle, and

calculating the sine of angle Ain the shaded triangle

shown (with the same peripheral angle A) establishes: