336 Menelaus of Alexandria

Menelaus’s theorem

mA+ mB+ mC

–––––

–

2

As a variation of H

ERON

’

S FORMULA

, the area of a

triangle can be expressed solely in terms of the lengths

of the medians of the triangle. We have:

where mA, mB, and mCare the lengths of the three

medians and s= .

See also

AAA

/

AAS

/

ASA

/

SAS

/

SSS

; A

POLLONIUS

’

S THEO

-

REM

; E

ULER LINE

.

Menelaus of Alexandria (ca. 70–130) Greek Geome-

try, Trigonometry Born in Alexandria, Egypt, mathe-

matician Menelaus is noted for his only surviving work

Sphaerica (Spheres), which contains the earliest known

results on

SPHERICAL GEOMETRY

and spherical trigonom-

etry. By converting spherical results into planar ones,

Menelaus also established a number of significant theo-

rems about planar geometry, including the famous result

that now bears his name.

Extremely little is known of Menelaus’s life.

Despite being cited throughout history as a native of

Alexandria, it is known that Menelaus spent some por-

tion of his life in Rome. For instance, records from the

year 98 list a number of astronomical observations

made by Menelaus from that city at that time.

Menelaus’s work in spherical geometry was likely

inspired by his work in astronomy. The first of the

three volumes of Sphaerica defines the basic principles

of the subject and includes the very precise definition of

a spherical triangle as one made by three arcs of great

circles, each less than a semicircle. Following the same

level of rigor as established by the geometer E

UCLID

,

Menelaus developed the theory of this geometry in con-

siderable depth with precise logical reasoning. (Curi-

ously, Menelaus eschewed any use of

PROOF BY

CONTRADICTION

, an approach that Euclid freely used.)

In volume II of Sphaerica, Menelaus developed applica-

tions to astronomy, and in volume III explored spheri-

cal trigonometry and applications to plane geometry.

Arab scholars of the period 850–1500

C

.

E

. trans-

lated Menelaus’s work and wrote many commentaries

on the piece. The same scholars also made reference to

other texts by Menelaus, including pieces called Chords

in a Circle and Elements of Geometry, as well as a

comprehensive text on the topic of mechanics. Sadly,

no copies of these works survive today.

See also A

RABIC MATHEMATICS

; M

ENELAUS

’

S

THEOREM

.

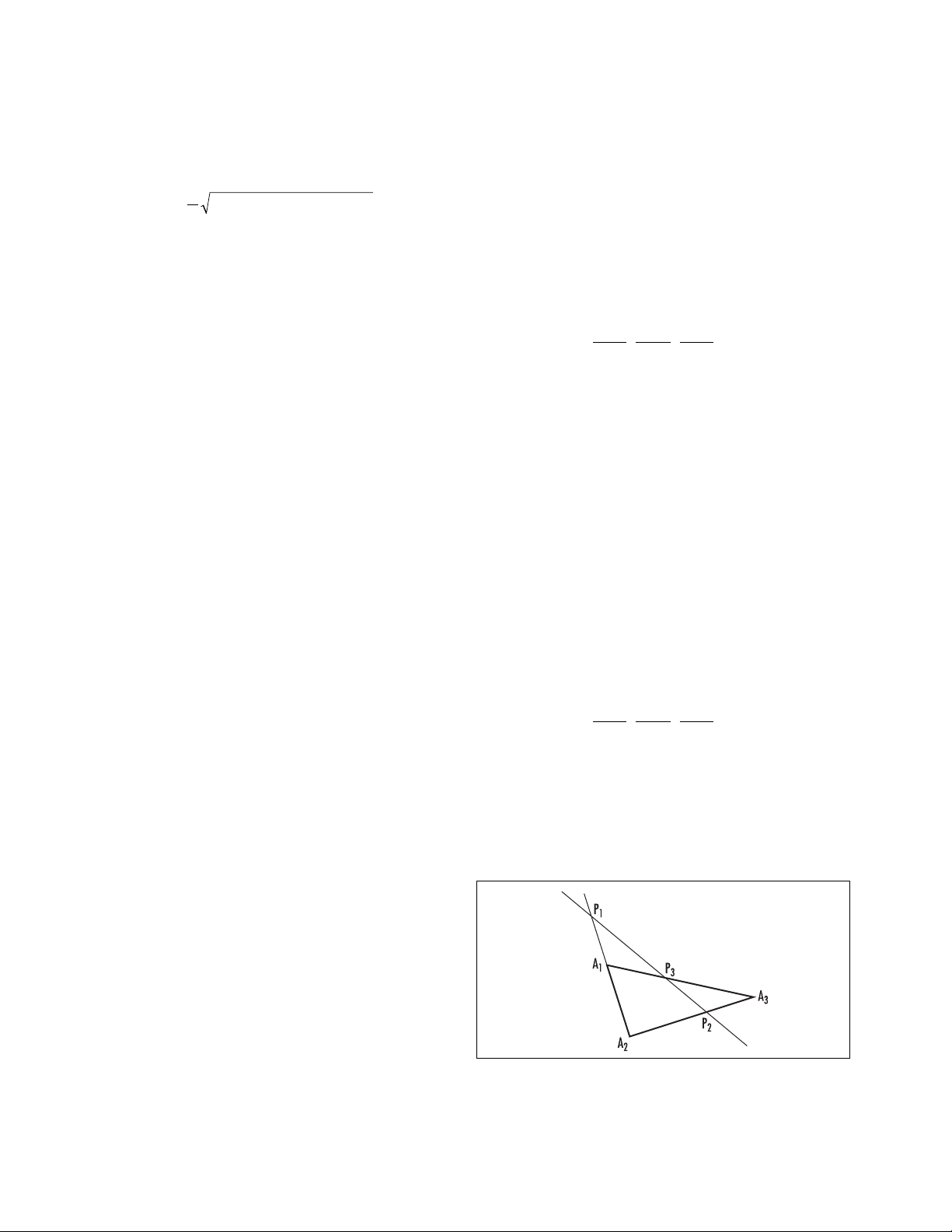
Menelaus’s theorem Suppose a

TRANSVERSAL

cuts

the three sides of triangle A1A2A3at points P1,P2, and

P3as shown:

Then, if AiPjrepresents the length of the line seg-

ment connecting point Aito point Pj, we have:

This result was first observed by the Greek mathe-

matician M

ENELAUS OF

A

LEXANDRIA

(ca. 70–130

C

.

E

.).

He proved it by drawing lines from each vertex Aito

the transversal to yield five right-angled triangles.

Examining the angles within these triangles shows that

a number of these triangles are similar. Chasing

through all the pairs of sides that consequently are in

the same ratio eventually establishes the result.

The converse of Menelaus’s theorem is also true:

If P1, P2, and P3are three points on the sides

of a triangle A1A2A3, with P1on side A1A2

(possibly extended), P2on side A2A3(possibly

extended), and P3on side A3A1(possibly

extended), satisfying

then the three points are

COLLINEAR

.

See also

AAA

/

AAS

/

ASA

/

SAS

/

SSS

; C

EVA

’

S THEOREM

.