√x2+ (y– a)2

paraboloid 373

Parabola

1

–

2

2a

–––

x

x

––

2a

1

––

4a

1

––

4A

1

––

4A

any

CONIC SECTION

, then the three points of intersec-

tion of opposite pairs of sides lie on a straight line. (A

pair of two straight lines can be thought of as a degen-

erate

HYPERBOLA

.)

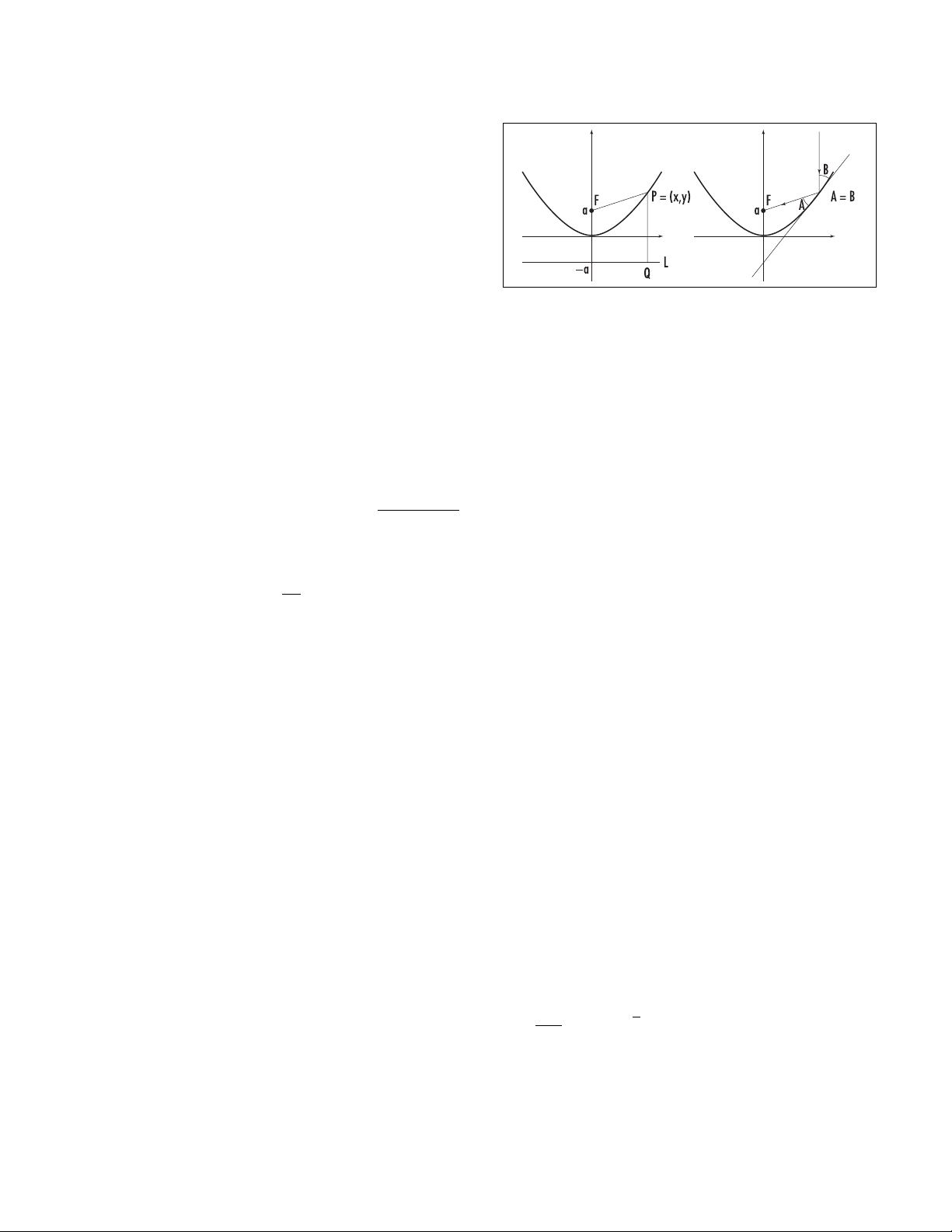
parabola As one of the three

CONIC SECTIONS

, a

parabola is the plane curve consisting of all points P

that are equally distant from a given fixed point F, and

a given fixed line L. The fixed point is called the focus

of the parabola, and the fixed line its directrix. A

parabola also arises as the curve produced by the inter-

section of a plane through a right circular

CONE

held

parallel to the slant side of the cone.

The equation of a parabola can be found by intro-

ducing a coordinate system in which the focus is the

point F= (0,a), for some positive number a, and the

directrix is the horizontal line y= –a. If P= (x,y) is an

arbitrary point on the parabola, then the

DISTANCE FOR

-

MULA

describes the defining condition as =

y+ a. Squaring and simplifying yields the equation:

Conversely, reversing these steps shows that any

equation of the form y= A(x– p)2+ qis the equation

of a parabola with focus F= (p,q+ ) and directrix

y= q– . Thus the graph of any quadratic equation

is a parabola.

The reflection property of a parabola states that

any incoming ray of light perpendicular to the directrix

will be reflected directly to the focus F. On the diagram

above right, this means that the angles to the tangent

line to the curve Aand Bare equal. (This can be proved

with

CALCULUS

by noting that, at the point P= (x,y),the

slope of the tangent line to the parabola y= x2is

m1= , whereas the slope of the line connecting the

point Qto F, is m2=–. Since m1m2= –1, these lines

are perpendicular. This shows that the tangent line

bisects the isosceles triangle FPQ, yielding that angles

Aand Bare equal.) Satellite dishes and reflecting tele-

scopes use dishes with parabolic cross-sections so as to

focus parallel rays of light to a fixed point, and con-

versely, search-light reflectors and automobile headlight

reflectors, for example, are parabolic: all rays from a

bulb positioned at the focus are reflected parallel to the

axis of the parabola. (See

PARABOLOID

.)

Parabolas appear in the folding of a thin sheet of

paper. Draw a dark straight line on the sheet—this will

be the directrix of the parabola—and a dot not on the

line, the focus. Fold the dot onto the line and crease the

paper. Open up the fold and do this again, this time

folding the dot to a different point on the line. As you

do this many times, the shape of a parabola emerges

along the side of all the creases.

A parabola is said to have

ECCENTRICITY

eequal to

1. The ratio of the distance of a point Pon the curve

from a fixed point (the focus) to its distance from a

fixed line (the directrix) is always 1.

See also A

POLLONIUS

’

S CIRCLE

;

ELLIPSE

;

HYPERBOLA

.

paraboloid The

SOLID OF REVOLUTION

obtained by

rotating a

PARABOLA

about its axis is called a

paraboloid. The points on its surface satisfy an equa-

tion of the form z= b(x2+ y2), where bis a constant,

and each horizontal cross-section, or each

CONTOUR

LINE

, of the solid is a circle. The shape of the figure

resembles a bowl.

Techniques of

INTEGRAL CALCULUS

show that the

volume of a section of the solid, up to a height h, is

given by V= πa2h, where ais the radius of the

circular cross-section at height h. It’s surface area is

.

Each vertical cross-section of the paraboloid is,

of course, a parabola. The common focus of these