lengths of the seasons and the timing of the solstices
and equinoxes, Ptolemy concluded that, although, in
his belief, the Sun orbits the Earth, the Earth does not
lie at the center of that orbit. He develops a mathemati-
cal theory to calculate the distance from that center
that the Earth supposedly lies.
Books 4 and 5 examine the motion of the Moon,
and Book 6 provides a theory of eclipses. Much of
Books 7 and 8 represent a catalogue of over 1,000 stars,
and the remaining five books explore his epicyclic the-
ory of planetary motion.
Ptolemy also wrote important scientific works in
other fields. His book Analemma discusses novel math-
ematical methods for constructing sundials; his work
Optics examines properties of color, reflection, and
refraction; and his major work Geography attempts to
map the entire world known at his time, giving mea-
surements as accurate as possible for the latitude and
longitude of major cities.
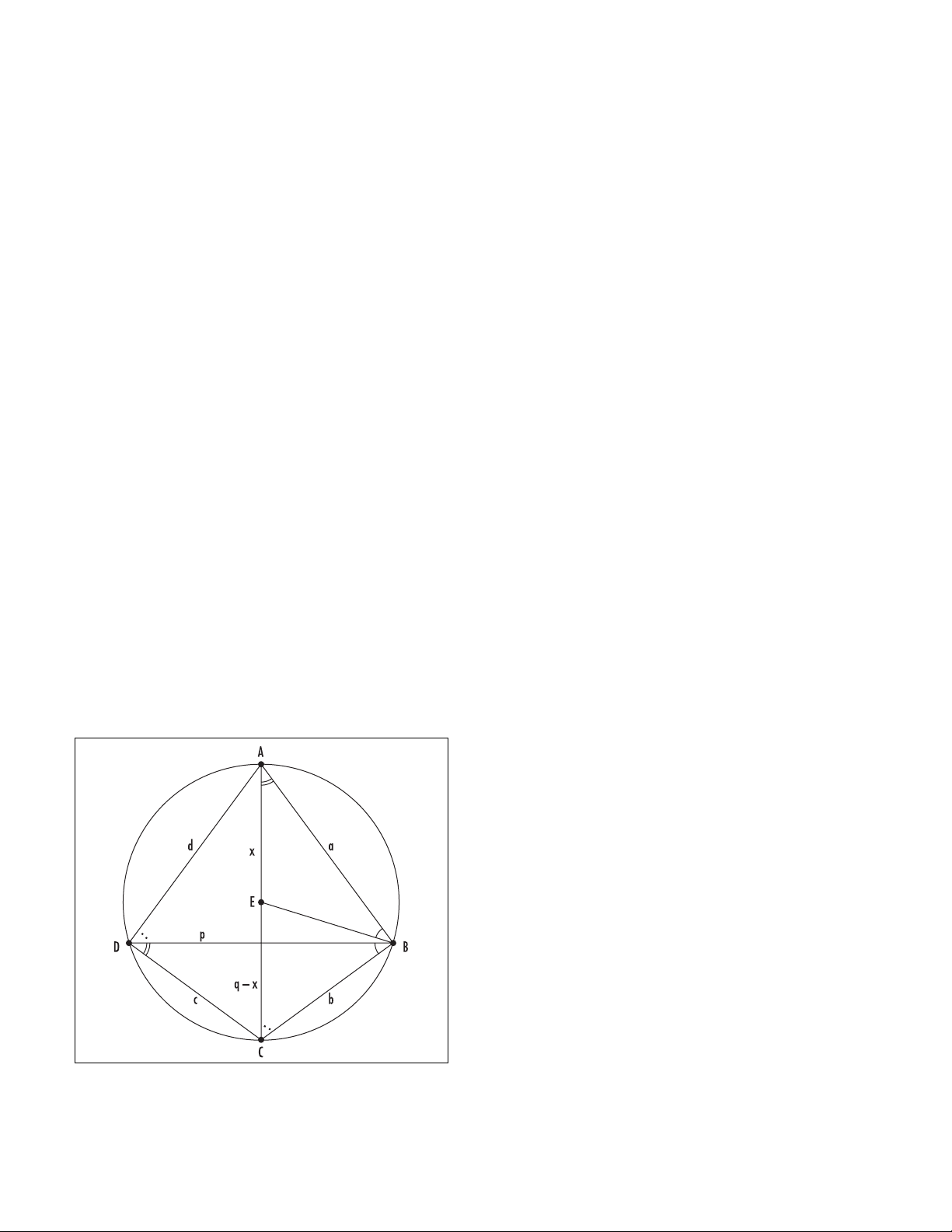
Ptolemy’s theorem Second-century Greek astronomer
and mathematician C
LAUDIUS
P
TOLEMY
proved the fol-
lowing result, now known as Ptolemy’s theorem:
If a, b, c, and dare the side-lengths of a
QUADRILATERAL
inscribed in a circle, and if p
and qare the lengths of its diagonals, then ac
+ bd = pq.
It can be proved as follows: according to the standard
CIRCLE THEOREMS
, angles CAB and CDB shown are
equal. Construct line BE so that triangles ABE and
CBD are similar. Then = . One then checks that
triangles ABD and EBC are also similar (angles ADB
and ACB are equal), and so = . Consequently
ac + bd = px + p(q– x) = pq.
See also B
RAHMAGUPTA
’
S FORMULA
;
SIMILAR
FIGURES
.
pure mathematics The study of abstract mathematical
systems and structures, without necessarily having practi-
cal applications in mind, is called pure mathematics. It
has various branches, including
ABSTRACT ALGEBRA
,
GEOMETRY
,
NUMBER THEORY
,
CALCULUS
,
TOPOLOGY
,
and the topics derived from them, but the distinction
from
APPLIED MATHEMATICS
might not be sharp. For
example, E
UCLIDEAN GEOMETRY
could be analyzed as
an abstract study of the relationships between lines,
points, and geometric shapes based on the foundations
of E
UCLID
’
S POSTULATES
, or could, at the same time, be
viewed as a study of results that could potentially (and,
in fact, has proved to be) useful to architects, survey-
ors, engineers, and scientists.
Although much of the mathematics developed in
the time of antiquity was clearly motivated by practical
concerns, the development of mathematics for its own
sake was nonetheless of interest to early scholars. For
instance, Babylonian tablets from ca. 1600
B
.
C
.
E
. list
large P
YTHAGOREAN TRIPLES
that could have no practi-
cal use. Greek mathematicians of around 400
B
.
C
.
E
.
began to seek rigor, proof, and justification in their
mathematical thinking, and ca. 300
B
.
C
.
E
.E
UCLID
pro-
duced his logically rigorous treatise T
HE
E
LEMENTS
,
summarizing all mathematical knowledge known at his
time. The unique organization of ideas presented in his
work became the key feature of the piece. That, in
itself, was seen as an analysis of logical thinking, one
that became the paradigm of all mathematical and sci-
entific thinking for the two millennia that followed.
During the 19th century, mathematicians began to
search for unifying ideas between distinct branches of
algebra and geometry. The general study of structures
and operations on them led to the development of
abstract algebra, for instance. The development of
PARA
-
DOX
es in
SET THEORY
and in the foundations of
p
–
d
b
––
q – x
p
–
c
a
–
x
422 Ptolemy’s theorem
Ptolemy’s theorem