430 quadrilateral

Quadrilaterals

This is a factorization with integral coefficients.

For the quadratic expression 8x2+ 2x– 3, we

selected p= –4 and q= 6. Then d= gcd(8,–4) = 4 and

e= gcd(–3,6) = 3, again yielding the factorization

.

A quadratic form is a homogeneous polynomial of

degree two. For example, ax2+ bxy + cy2is a quadratic

form in two variables. A quadratic curve is a curve

given by an algebraic equation of second degree. For

example, a

CIRCLE

, given by an equation of the form

(x– a)2+ (y– b)2= r2, is a quadratic curve.

See also

HISTORY OF EQUATIONS AND ALGEBRA

(essay).

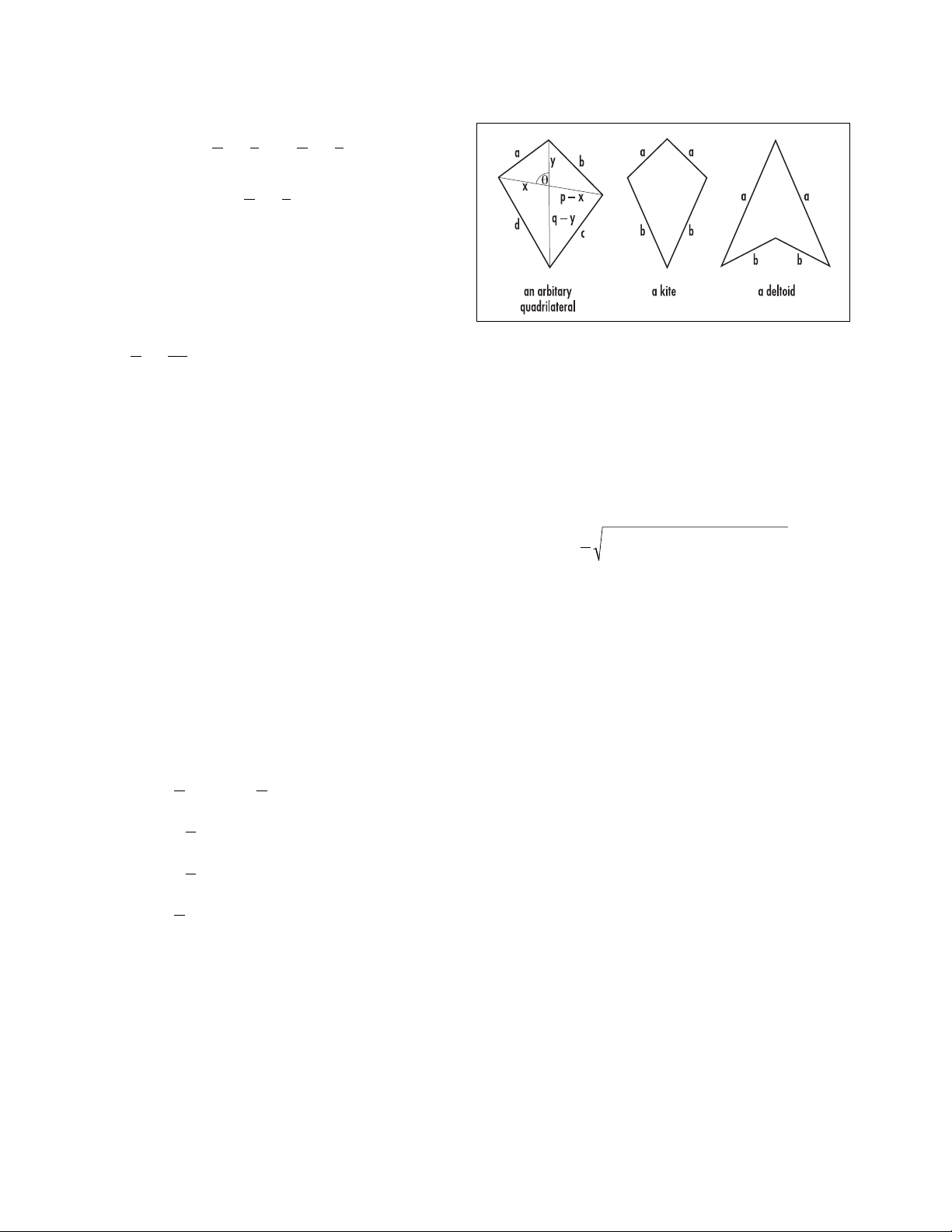
quadrilateral (quadrangle, tetragon) Any

POLYGON

with four sides is called a quadrilateral. For example,

any

SQUARE

,

TRAPEZIUM

, or

PARALLELOGRAM

is a

quadrilateral. Kites and deltoids are quadrilaterals

whose adjacent sides are equal in pairs.

If pand qare the lengths of the diagonals of a con-

vex quadrilateral, and θis the angle between them,

then the

AREA

of the quadrilateral is given as the sum

of the areas of the four triangles they create:

Applying the

LAW OF COSINES

to each the four triangles

and summing yields the second equation:

b2+ d2– a2– c2= 2pqcos(θ).

(Here a, b, c and dare the side-lengths of the quadri-

lateral as shown in the diagram.) Solving for sin(θ) in

the first equation and for cos(θ) in the second and

substituting into the equation cos2(θ)+sin2(θ) = 1, a

standard identity in

TRIGONOMETRY

, yields one ver-

sion of B

RETSCHNEIDER

’

S FORMULA

for the area of a

quadrilateral:

Analogous arguments show that these two formulae

for area hold for concave quadrilaterals also.

A quadrilateral is called a cyclic quadrilateral if it

is a

CYCLIC POLYGON

, that is, if its four vertices lie on a

circle. A consequence of the

CIRCLE THEOREMS

shows

that opposite interior angles of a cyclic quadrilateral

sum to 180°. The area of a cyclic quadrilateral is given

by B

RAHMAGUPTA

’

S FORMULA

.

Every quadrilateral, no matter its shape, provides a

TESSELLATION

of the plane, that is, copies of any single

quadrilateral tile can be used to cover the entire plane

without overlap.

See also

CONCAVE

/

CONVEX

; P

TOLEMY

’

S THEOREM

.

quantifier In English, we frequently encounter state-

ments containing the words all, some, and no (or

none). These words are called quantifiers. For example,

“All math books are boring,” “Some lakes contain

fresh water,” and “No poet plays the viola” are quanti-

fied statements.

Mathematicians reduce all quantified statements to

two standard forms by use of either the universal quan-

tifier: “for all,” denoted , or the existential quantifier:

“there exists,” denoted ∃. For example, the statement

A