√
–
3
––
2
1
–
2
1
––
√
–
2
trigonometry 509
The sine and cosine of a positive and a negative angle
Relating trigonometry to triangles
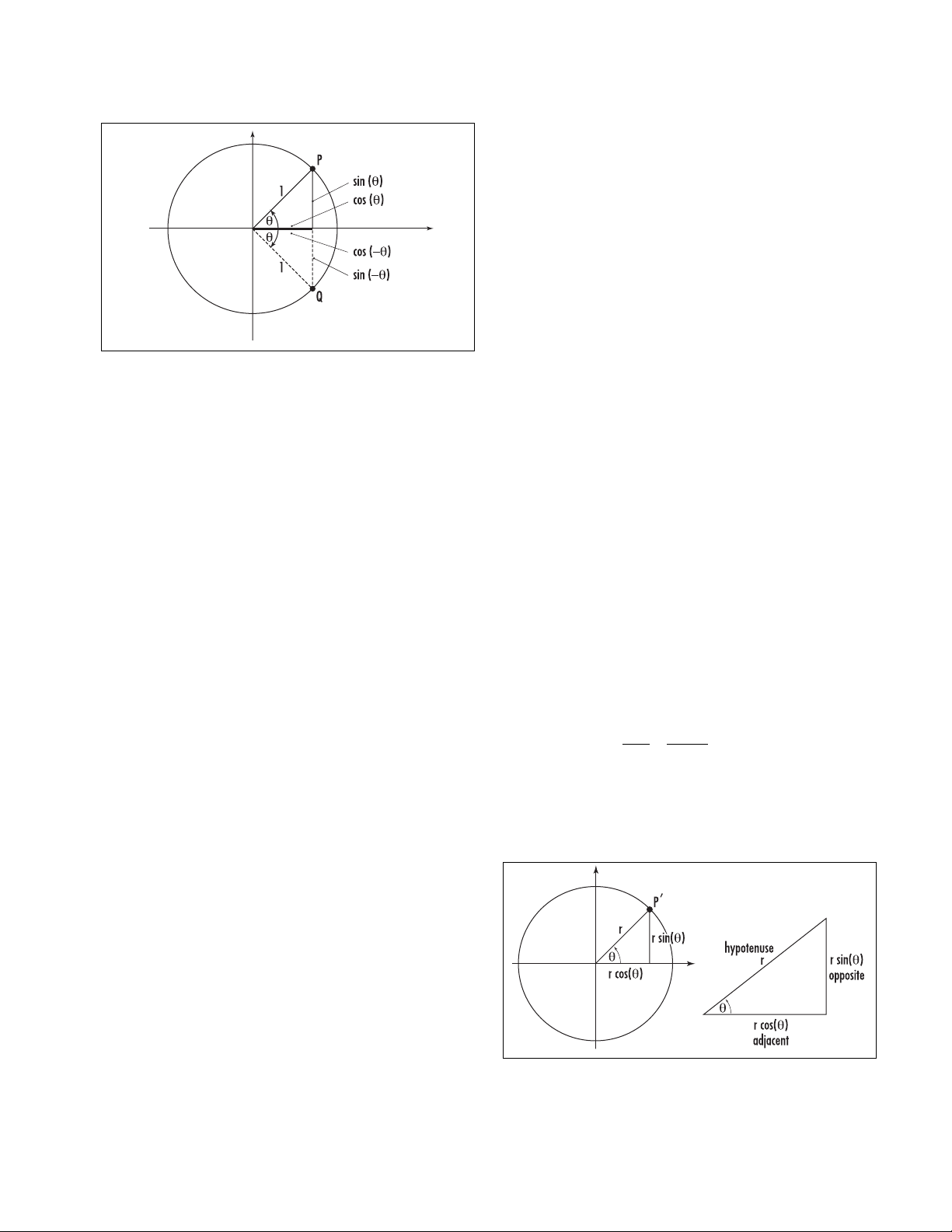
point on that circle located at a particular angle θ. It
has become the convention to measure angles in rela-
tion to the positive x-axis, with a positive angle inter-
preted as a counterclockwise turn and a negative angle
as a clockwise turn. The y-coordinate of a point on the
circle is the sine (abbreviated “sin”) of the angle at
which that point lies, and the x-coordinate is the com-
panion value cosine (abbreviated “cos”). Thus a point
Plocated at angle θhas coordinates P= (cos(θ), sin(θ)).
A point Qlocated at angle –θhas coordinates Q=
(cos(–θ), sin(–θ)).
We see from the diagram that the sine and cosine
functions satisfy the relations:
cos(–θ) = cos(θ)
sin(–θ) = –sin(θ)
Also, P
YTHAGORAS
’
S THEOREM
gives (sin(θ))2+
(cos(θ))2= 1. Following the convention of writing
(sin(θ))nas sinnθ, this reads:
sin2θ+ cos2θ= 1
Note that adding or subtracting a multiple of 360°
(or, if using radian measure, any multiple of 2π) to an
angle does not change the location of the point on the
UNIT CIRCLE
it represents. We have:
cos(θ+ 360k) = cosθ
sin(θ+ 360k) = sinθ
for any whole number k.
It is possible to compute the sine and cosine of
some simple angles. For instance, a point located at
angle θ= 0 degrees lies at position (1,0), and so cos(0)
= 1 and sin(0) = 0. Similarly, the point at angle θ= 90°
has coordinates (0,1) yielding cos(90) = 0 and sin(90)
= 1. A point at angle θ= 45°lies at one vertex of an
isosceles right triangle, showing that sine and cosine
values for 45°are equal. Pythagoras’s theorem tells
us that cos(45) = sin(45) = . Similarly, a point at
angle θ= 60 lies at the apex of half an equilateral
triangle of side-length 1. We obtain cos(60) = and, by
Pythagoras’s theorem, sin(60) = . These values are
reversed for an angle of 30°.
Connection to Larger Circles and to Triangles
If one enlarges the diagram of the unit circle by a
SCALE
factor r, then all lengths in that diagram increase by
that factor r. Consequently, the coordinates of a point
P′located at an angle θon a circle of radius r(still cen-
tered about the origin) is given by the values cos θand
sinθmultiplied by r. We have P′= (rcos θ, rsin θ).
Within the diagram lies a right triangle with one
angleθand hypotenuse equal to r. The side opposite
angle θhas length rsinθ, and the remaining side adja-
cent to the angle has length rcos θ. Notice that the ratio
“opposite over hypotenuse” has value sin θ:
Similarly, the ratio “adjacent over hypotenuse” yields
cosθ:
opp
hyp ==
r
r
sin sin
θθ