circle at the point M= (1,0). Extend the radius
OP further until it meets the tangent line at Q.
Then tan θis the length of the tangent line-
segment MQ and sec θis the length of the
secant to the circle OQ.
Dividing the Pythagorean identity sin2θ+ cos2θ= 1
through by cos2θand by sin2θyields the identities:
1 + tan2θ= sec2θ
1 + cot2θ= csc2θ
The Addition and Subtraction Formulae
The diagram on the following page shows that two
congruent copies of a right triangle containing an angle
Aand two copies of a second right triangle containing
an angle Bcan be arranged in the same large rectangle
in two different ways.
The
AREA
of the region surrounding the four trian-
gles, which must be the same for each diagram, can be
computed as the sum of areas of two rectangles or as
the area of a
PARALLELOGRAM
of base of length 1, and
height of length cos(A– B). This yields the difference
formula for cosines:
cos(A– B) = cos A cos B+ sin A sin B
Substituting in –Bfor B, yields the addition formula for
cosines:
cos(A+ B) = cos A cos(–B) + sin A sin(–B)
= cos A cos B– sin A sin B
trigonometry 511
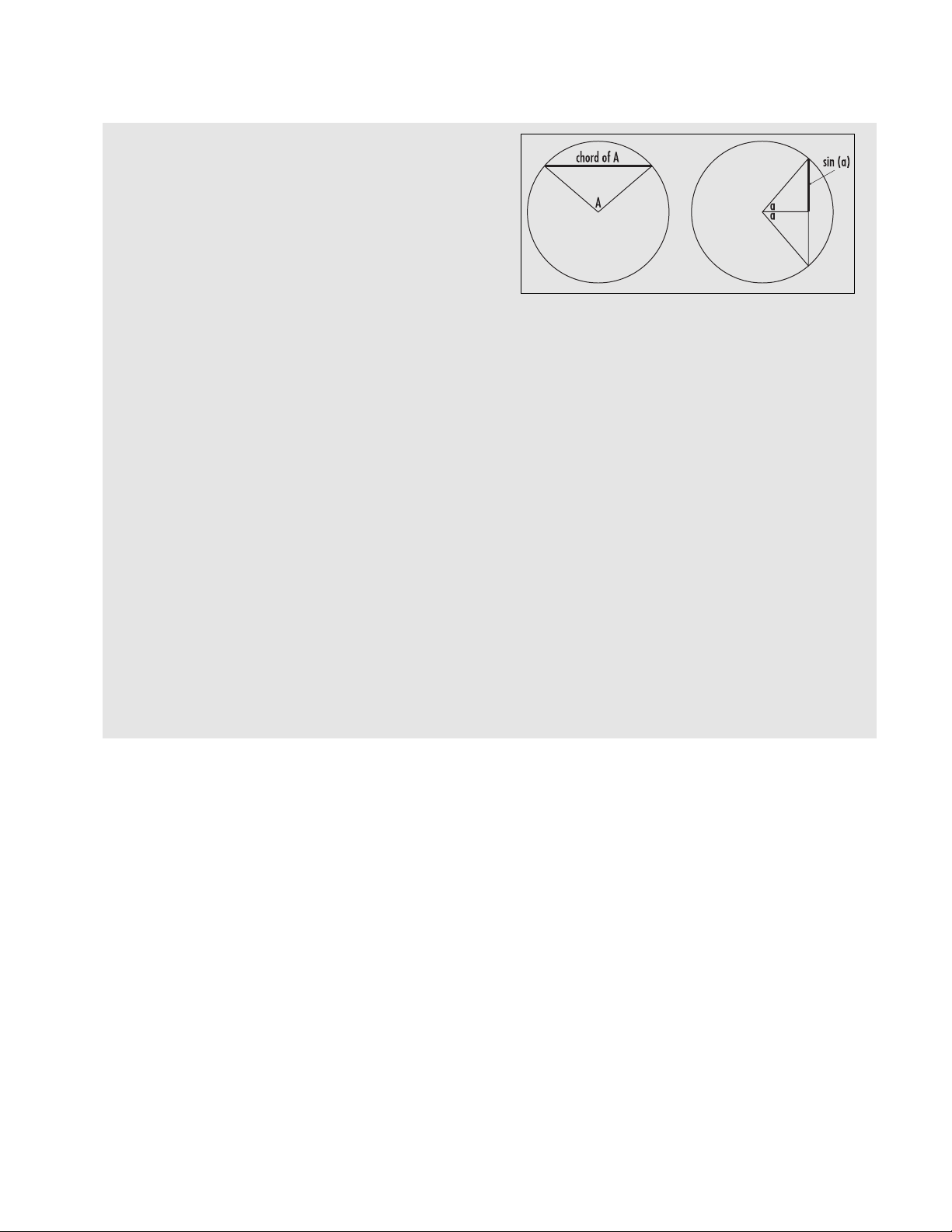
translate the Sanskrit word jy –
a, into their texts and simply
wrote jiba as a close approximation.
In the 12th century, European scholars began translat-
ing the Arabic works and soon became acquainted with the
extensive theory of trigonometry. Misinterpreting jiba as the
Arabic word jaib for “cove” or “bay,” translators wrote the
Latin equivalent sinus as the name of the half-chord quan-
tity. From this we have the name “sine.”
The famous scholar F
IBONACCI
(ca 1170–1250) also trav-
eled extensively in the Arab countries and wrote of their
trigonometry in his famous work Practica geometriae.
Around 1464, the German astronomer and mathematician
R
EGIOMONTANUS
(1436–76) compiled De triangulis omnimodis,
a compendium of trigonometry of that time. This work was
enormously influential, and over the following decades other
texts on the topic appeared. German mathematician Georg
Joachim Rhaeticus (1514–74) published, in 1551, Canon doc-
trinae triangulorum, which defined, for the first time, all six
basic trigonometric functions, and explained how to relate
them to right triangles without making any reference to cir-
cles. Danish physician Thomas Fincke (1561–1656), in his
work Geometriae rotundi, coined the terms tangent and
secant, and developed further fundamental trigonometric
formulae. The word trigonometry itself was invented by Ger-
man mathematician Bartholomaeus Pitiscus (1561–1613) in
his treatise Trigonometria: sive de solutione triangulorum
tractatus brevis et perspicuus. By this time, trigonometry
was certainly regarded as a worthwhile topic of mathemati-
cal pursuit, independent of applications to astronomy.
The subject also proved to be useful in the study of
algebra. French mathematician F
RANÇOIS
V
IÈTE
(1540–1603)
showed, for example, that one could solve certain cubic
equations by making trigonometric substitutions. His
famous formula for πcan be derived with repeated use of
trigonometric functions.
Up until this point, sine values, as well as the other
trigonometric values, were still regarded as actual line
lengths and not ratios of lengths. After the invention of
CALCU
-
LUS
, L
EONHARD
E
ULER
(1707–83) came to realize that it is appro-
priate to think of sine not as a physical length, but rather as a
function of angle independent of length. He suggested that
this could be accomplished by scaling all circles under con-
sideration to unit circles, an operation that is equivalent to
dividing all quantities by the radius of the circle. Thus, for the
first time, all trigonometric quantities came to be thought of
as ratios, In 1748 Euler wrote Introductio in analysin infinito-
rum, which became the dominating textbook on the topic of
trigonometry for the century that followed. It essentially out-
lines the principles of trigonometry as we regard them today.
Chords and half-chords