514 truth table

pq pqp∨qp→qp↔q

TT T T T T

TF F T F F

FT F T T F

FF F F T T

∨

p

¬

p

TF

FT

pqr p (q—> r)

TTT TTTTT

TTF TFTFF

TFT TTFTT

TFF TTFTF

FTT FFTTT

FTF FFTFF

FFT FFFTT

FFF FFFTF

(4) (5) (1) (3) (2)

^

differential equation has

trivial solution y= 0. Any solution to a problem that

may be of interest is called nontrivial. For example, the

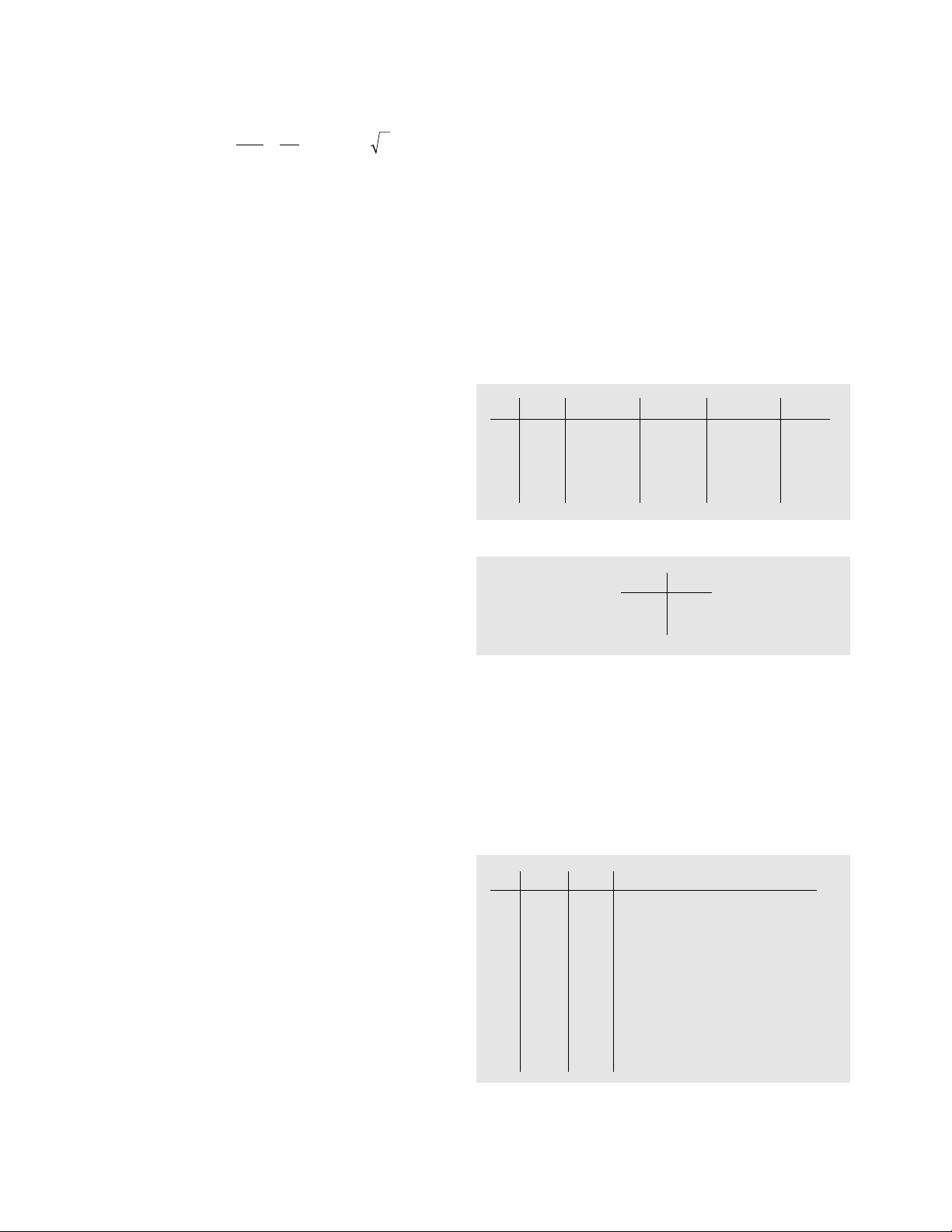
equation x3– 2x= 0 has nontrivial solution x= √

–

2.

The word trivial comes from the Latin word triv-

ium, the medieval name for the three least-complicated

of the seven subjects of study offered in medieval uni-

versities: grammar, rhetoric, and logic. (The remaining

four subjects—arithmetic, astronomy, geometry and

music—were known as the quadrivium.)

Mathematicians often use the word trivial to

describe a result that requires little or no effort to

prove. For example, that any multiple of 4 is divisible

by 2 would be deemed a trivial result.

truth table In the field of

FORMAL LOGIC

, proposi-

tional calculus is the name given to the analysis of truth-

values of complicated statements built up from simpler

statements linked together via the connectives and; or; if

… then …; and if, and only if (called, respectively, the

CONJUNCTION

, the

DISJUNCTION

, the

CONDITIONAL

, and

the

BICONDITIONAL

). One can also consider the

NEGA

-

TION

of a statement.

For example, the statement “The moon is round

and is made of green cheese” is a compound statement

made of two simpler statements (“The moon is round”

and “The moon is made of green cheese”) linked

together via the connective and. The truth-value of the

statement as a whole depends on the truth-value of the

two individual statements of which it is composed.

In symbols, statements are usually represented as

lowercase letters (p,q,r, for example), and the connec-

tives combining them are denoted:

pand q: p q

por q: p ∨q

If pthen q: p →q

pif, and only if, q: p ↔q

not p:

¬

p

A compound statement is a statement built up

from simpler statements via connectives. For example,

p(q→r) and p∨(

¬

p)

are compound statements. (Parentheses are used to

indicate the order in which the connectives are to be

applied.) For example, if pis the statement “The moon

is round,” qthe statement “The moon is made of green

cheese,” and rthe statement “The moon is edible,”

then p(q→r) can be interpreted as, “The moon is

round AND, IF the moon is made of green cheese,

THEN it is edible.” The statement p∨(

¬

p) can be

interpreted as “The moon either is or is not round.”

A truth table is a table showing the truth-value of a

statement (typically a compound one) given the possi-

ble truth-values of the simple statements of which it is

composed. The truth-values of the basic connectives are

given as follows:

(The truth-values presented here are motivated by intu-

ition. See

CONJUNCTION

,

DISJUNCTION

,

CONDITIONAL

,

BICONDITIONAL

, and

NEGATION

for details.) The truth-

value of any compound statement is now completely

determined. The procedure is mechanical. For example,

the compound statement p(q→r) has the follow-

ing truth table, given in bold:

∨

∨

∨

∨