volume 527

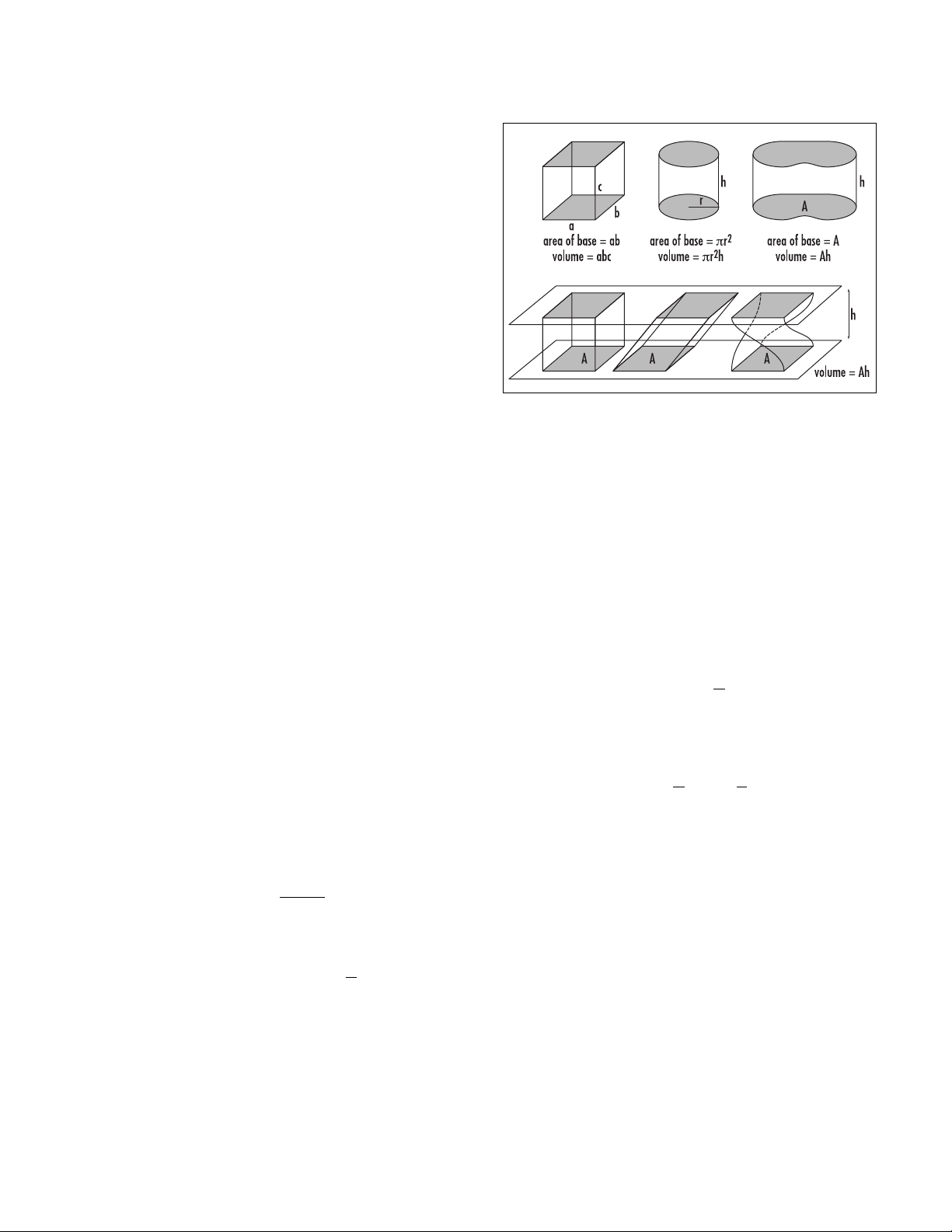
The volume of figures

√r2+ x2

2

circular base of radius rhas base area πr2and thus a

volume πr2h.

This point of view imagines volumes as well approxi-

mated by stacks of thin layers of “volume,” each a hori-

zontal cross-section of solid that is the same size and

shape as the base. Like a deck of 52 cards stacked to pro-

duce a rectangular box, the volume of a stack of sheets

does not change if the pile is skewed: the shape of the

deck may change, but its volume does not. This observa-

tion was first noted by 17th century Italian mathemati-

cian B

ONAVENTURA

C

AVALIERI

(1598–1647). It leads to a

general principle, today called C

AVALIERI

’

S PRINCIPLE

:

Solids of equal height have equal volumes if sec-

tions made by planes parallel to the base at the

same distance from the base have equal areas.

Techniques of

INTEGRAL CALCULUS

are used to

compute volumes. The methods here are really no dif-

ferent than approximating solids again as stacks of thin

cards or, perhaps, as collections of small boxes (whose

volumes are known) and taking the

LIMIT

as better and

better approximations are made.

For example, suppose a solid has height hand that

the area of a cross section made by a plane parallel to the

base at height xis A(x).Imagine we slice the solid into

thin “cards” at positions 0 = x0< x1< … xn–1 < xn= h.

Then the volume Vof the solid can be well approximated

as the sum of volumes of cards of base area A(xi) and

width xi+1 – xi, that is, . Taking

the limit as more and more values between 0 and hare

chosen (that is, as thinner and thinner cards are used)

gives the true volume of the solid as an integral:

V= ∫h

0A(x)dx

For instance, the cross section of a sphere of radius rat

a distance xfrom the plane running through the equa-

tor is a circle of radius and area π(r2– x2).

Thus the volume of a sphere of radius ris:

Any cross section of a

CONE

with base of an arbi-

trary shape is a scaled version of the same planar shape.

At half the distance from the apex of the cone, the cross

section has area one-quarter the area of the base. At

one-third the distance from the apex, the cross section

has area one-ninth the area of the base. In general, if the

area of the base is Aand the height of the cone is h,

then the area of the cross section at a distance xfrom

the apex has area A(x) = A×. The volume of any

cone with base of area Aand height his thus:

The volume of a

FRUSTUM

can be calculated the same

way.

The word volume comes from the Latin volumen,

meaning “scroll,” where the size or the bulk of a book

eventually led to the use of the word for the size or

bulk of any object.

See also

DOUBLE INTEGRAL

;

SCALE

;

SOLID OF

REVOLUTION

.