“unique factorization domain”的概念、定义、习题解题方法及翻译-数学辞典

单词

unique factorization domain

释义

unique factorization domain

(UFD) The Fundamental Theorem of Arithmetic shows that an integer greater than 1 can be uniquely factorized into primes; a unique factorization domain is essentially a ring in which the fundamental theorem holds. Specifically, an integral domain R is a UFD if

(i) every non-zero element, which is not a unit, can be written as a product of irreducible elements;

(ii) if p1p2…pm = q1q2…qn, where the pi and qj are irreducible, then m = n and (with possible reordering) for each i we have pi = uiqi for some unit ui.

In a UFD, an element is prime if and only if it is irreducible. If R is a UFD, then R[x] is also a UFD. Euclidean domains are UFDs.

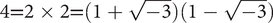Note in $inline$ that $inline$ are two essentially different factorizations of 4, and so R is not a UFD. By contrast, R[x], the ring of real polynomials in a variable x, is a UFD. Note that 2x2 − 6x + 4 = (2x − 2)(x − 2) =(x − 1)(2x − 4), but these are essentially the same factorization as (2x − 2) = 2(x − 1) and (x − 2) = 2−1(2x − 4), and 2 is a unit in R[x].

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。