Venn diagram
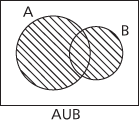
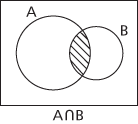
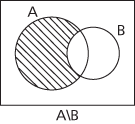
Given one set, A, the universal set is divided into two disjoint subsets A and A′, which can be clearly seen in a simple Venn diagram. Given two sets A and B, the universal set E is divided into four disjoint subsets A ∩ B, A′ ∩ B, and A ∩ B′ and A′ ∩ B′. A Venn diagram drawn with two overlapping circles for A and B clearly shows the four corresponding regions. Given three sets A, B and C, the universal set E is divided into eight disjoint subsets A ∩ B ∩ C, A′ ∩ B ∩ C, A ∩ B′ ∩ C, A ∩ B ∩ C′, A ∩ B′ ∩ C′, A′ ∩ B ∩ C′, A′ ∩ B′ ∩ C, and A′ ∩ B′ ∩ C′, and these can be illustrated in a Venn diagram as shown here.
Venn diagram with three sets
Venn diagrams can be illustrative but should generally be avoided for careful proofs, because a diagram may only illustrate a special case. Four general sets, for example, should not be represented by four overlapping circles because they cannot be drawn in such a way as to make apparent the 16 disjoint subsets into which E should be divided. See also truth tables.
- logarithmic function
- logarithmic plotting
- logarithmic scale
- logarithmic series
- logarithmic spiral
- logic
- logically equivalent
- logic gate
- logicism
- logistic map
- logistic map
- lognormal distribution
- log paper
- long division
- longitude
- longitudinal study
- longitudinal wave
- loop
- Lorentz force law
- Lorentz group
- Lorentz, Hendrik Antoon
- Lorentz transformation
- Lorentz–Fitzgerald contraction
- Lorenz attractor
- Lotka-Volterra equations