单词	curl
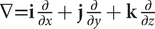释义	curl For a vector function of position V(r)=Vx i + Vy j + Vz k, the curl of V is the vector product of the operator del, with V giving curl which can be written in determinant form as 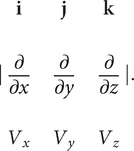If V = ∇φ then curlV = 0 and if the domain of V is simply connected then curlV = 0 implies V = ∇φ for a scalar field φ. Curl relates to the local rotation of a field; for example, if V is the velocity field of a fluid flow, a small ball of fluid will rotate in the direction of curlV, and with an angular speed half the magnitude of curlV. Compare divergence, gradient.
随便看	Borel set Borel–Cantelli Lemma Born, Max bottleneck problems bound boundary boundary condition boundary layer boundary value problem bounded above bounded below bounded function bounded sequence bounded set bounded space bounded variation Bourbaki, Nicolas Box-Jenkins model box plot bra braces brachistochrone brackets Brahmagupta Brahmagupta's formula

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。