determinant
The determinant of the 1×1 matrix [a] is simply equal to a. If A is the 2×2 matrix below, then detA = ad−bc, and the determinant can also be written as shown:
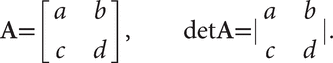
If A is a 3×3 matrix [aij], then det A, which may be denoted by

is given by
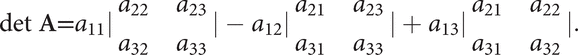
Notice how each 2×2 determinant occurring here is obtained by deleting the row and column containing the entry by which the 2×2 determinant is multiplied. This expression for the determinant of a 3×3 matrix can be written a11A11 + a12A12 + a13A13, where Aij is the cofactor of aij. This is the evaluation of detA, ‘by the first row'. In fact, detA may be found by using evaluation by any row or column: for example, a31A31 + a32A32 + a33A33 is the evaluation by the third row, and a12A12 + a22A22 + a32A32 is the evaluation by the second column. The determinant of an n×n matrix A may be defined similarly, as a11A11 + a12A12 + … + a1nA1n, and the same value is obtained using a similar evaluation by any row or column. These are known as the Laplace expansions of the determinant. However, calculating determinants this way is laborious; using elementary operations is much more efficient. The following properties hold: