“diagonalizable”的概念、定义、习题解题方法及翻译-数学辞典

单词

diagonalizable

释义

diagonalizable

(diagonalization) A square matrix is diagonalizable if it is similar to a diagonal matrix; that is, a square matrix A is diagonalizable if there exists an invertible matrix P such that P–1AP = D is diagonal. Equivalently A has an eigenbasis (which then forms the columns of P). A real matrix is diagonalizable if the roots of the characteristic equation are real and distinct, though the converse is not true (e.g. the identity matrix is diagonal). Generally a real matrix is diagonalizable if the roots of the characteristic equation are real and for each eigenvalue its algebraic multiplicity equals its geometric multiplicity. If P–1AP = D, then An = PDnP–1 and so powers of diagonalizable matrices can be easily calculated.

As examples: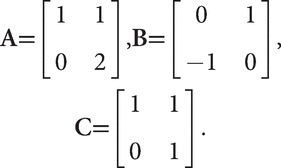

A is diagonalizable as it has distinct real eigenvalues (1 and 2); B is not diagonalizable as a real matrix as its characteristic polynomial x2 + 1 has no real roots, but B is diagonalizable as a complex matrix as x2 + 1 has distinct complex roots; C is not diagonalizable as the only eigenvalue 1 has algebraic multiplicity 2 and geometric multiplicity 1.

A linear map of a finite-dimensional vector space is diagonalizable if any matrix representing it is diagonalizable. See also minimal polynomial, spectral theorem, triangularizable.

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。