Fundamental Theorem of Game Theory
in a matrix game, with E(x,y) denoting the expectation, where x and y are mixed strategies for the two players, then
By using a maximin strategy (see conservative strategy), one player, R, ensures that the expectation is at least as large as the left‐hand side of the equation. Similarly, by using a minimax strategy, the other player, C, ensures that the expectation is less than or equal to the right‐hand side. Such strategies may be called optimal strategies for R and C. Since, by the theorem, the two sides of the equation are equal, then if R and C use optimal strategies the expectation is equal to the common value, which is called the value of the game.
For example, consider the game given by the matrix
if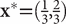 
, it can be shown that E(x,y)≥10/3 for all y. Also, if 
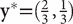, then E(x, y)≤10/3 for all x. It follows that the value of the game is 10/3, and x and y are optimal strategies for the two players.