hypergeometric distribution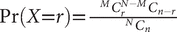 where r runs from 0 up to the smaller of M and n. This is called a hypergeometric distribution. The mean is
where r runs from 0 up to the smaller of M and n. This is called a hypergeometric distribution. The mean is 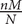 , and the variance is
, and the variance is
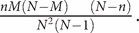
- expectation
- expectation
- expected monetary value
- expected utility
- expected value
- experiment
- experimental design
- explanatory variable
- explementary angles
- explicit function
- exploratory data analysis
- exponent
- exponential decay
- exponential distribution
- exponential function
- exponential function to base a
- exponential growth
- exponential of a matrix
- exponential series
- exponentiate
- express
- extended complex plane
- extended mean value theorem
- extended metric
- extended real numbers