Power Series
A power series in a variable ![]() is an infinite Sum of the form
is an infinite Sum of the form
 | (1) |
A Conjecture of Pólya is that if a Function has a Power series with IntegerCoefficients and Radius of Convergence 1, then either the Function isRational or the Unit Circle is a natural boundary.
A generalized Power sum ![]() for
for ![]() , 1, ... is given by
, 1, ... is given by
 | (2) |
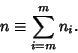 | (3) |
For any power series, one of the following is true:
- 1. The series converges only for
 .
. - 2. The series converges absolutely for all
 .
. - 3. The series converges absolutely for all
 in some finite open interval
in some finite open interval 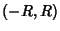 and diverges if
and diverges if  or
or 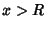 . At the points
. At the points 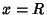 and
and 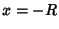 , the series may converge absolutely, converge conditionally, or diverge.
, the series may converge absolutely, converge conditionally, or diverge.
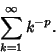 | (4) |
References
Arfken, G. ``Power Series.'' §5.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 313-321, 1985. Myerson, G. and van der Poorten, A. J. ``Some Problems Concerning Recurrence Sequences.'' Amer. Math. Monthly 102, 698-705, 1995. Pólya, G. Mathematics and Plausible Reasoning, Vol. 2: Patterns of Plausible Inference. Princeton, NJ: Princeton University Press, p. 46, 1954.
- Generalized Remainder Method
- General Linear Group
- General Orthogonal Group
- General Position
- General Prismatoid
- General Unitary Group
- Generating Function
- Generation
- Generator (Digitaddition)
- Generator (Group)
- Genetic Algorithm
- Genocchi Number
- Gentle Diagonal
- Gentle Giant Group
- Genus (Curve)
- Genus (Knot)
- Genus (Surface)
- Genus Theorem
- Geocentric Latitude
- Geodesic
- Geodesic Curvature
- Geodesic Dome
- Geodesic Equation
- Geodesic Flow
- Geodesic Triangle