Conic Section
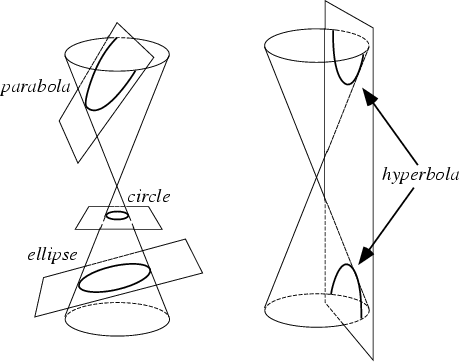
The conic sections are the nondegenerate curves generated by the intersections of a Plane with one or twoNappes of a Cone. For a Plane parallel to a Cross-Section, a Circle isproduced. The closed curve produced by the intersection of a single Nappe with an inclined Plane is anEllipse or Parabola. The curve produced by a Plane intersecting both Nappes is aHyperbola. The Ellipse and Hyperbola are known as Central Conics.
Because of this simple geometric interpretation, the conic sections were studied by the Greeks long before their applicationto inverse square law orbits was known. Apollonius 
wrote the classic ancient work on the subject entitled OnConics. Kepler was the first to notice that planetary orbits were Ellipses, andNewton was then able to derive the shape of orbits mathematically using Calculus, under the assumption thatgravitational force goes as the inverse square of distance. Depending on the energy of the orbiting body, orbit shapes whichare any of the four types of conic sections are possible.
A conic section may more formally be defined as the locus of a point 
that moves in the Plane of a fixed point 
called the Focus and a fixed line 
called the Directrix (with not on )such that the ratio of the distance of from to its distance from is a constant 
called theEccentricity. For a Focus 
and Directrix 
, the equation is
If
, the conic is a Parabola, if 
, the conic is an Ellipse, and if 
, it is aHyperbola.In standard form, a conic section is written
where
is the Radius of Curvature and is the Eccentricity. Five points in a plane determine a conic(Le Lionnais 1983, p. 56).See also Brianchon's Theorem, Central Conic, Circle, Cone, Eccentricity, Ellipse,Fermat Conic, Hyperbola, Nappe, Parabola, Pascal's Theorem, Quadratic Curve,Seydewitz's Theorem, Skew Conic, Steiner's Theorem
References
Besant, W. H. Conic Sections, Treated Geometrically, 8th ed. rev. Cambridge, England: Deighton, Bell, 1890. Casey, J. ``Special Relations of Conic Sections'' and ``Invariant Theory of Conics.'' Chs. 9 and 15 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 307-332 and 462-545, 1893. Coolidge, J. L. A History of the Conic Sections and Quadric Surfaces. New York: Dover, 1968. Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 138-141, 1967. Downs, J. W. Conic Sections. Dale Seymour Pub., 1993. Iyanaga, S. and Kawada, Y. (Eds.). ``Conic Sections.'' §80 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 271-276, 1980. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 56, 1983. Lee, X. ``Conic Sections.''http://www.best.com/~xah/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html Ogilvy, C. S. ``The Conic Sections.'' Ch. 6 in Excursions in Geometry. New York: Dover, pp. 73-85, 1990. Pappas, T. ``Conic Sections.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 196-197, 1989. Salmon, G. Conic Sections, 6th ed. New York: Chelsea, 1954. Smith, C. Geometric Conics. London: MacMillan, 1894. Sommerville, D. M. Y. Analytical Conics, 3rd ed. London: G. Bell and Sons, 1961. Yates, R. C. ``Conics.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 36-56, 1952.
Conic Sections
- Heron Triangle
- Herschel
- Herschfeld's Convergence Theorem
- Hessenberg Matrix
- Hesse's Theorem
- Hessian Covariant
- Hessian Determinant
- Heteroclinic Point
- Heterogeneous Numbers
- Heterological Paradox
- Heteroscedastic
- Heterosquare
- Heuman Lambda Function
- Heun's Differential Equation
- Heuristic
- Hexa
- Hexabolo
- Hexacontagon
- Hexacronic Icositetrahedron
- Hexad
- Hexadecagon
- Hexadecimal
- Hexaflexagon
- Hexagon
- Hexagonal Number