Affine Space
Let 
be a Vector Space over a Field 
, and let 
be a nonempty Set. Now define addition
for any Vector 
and element 
subject to the conditions
- 1.
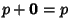, - 2.
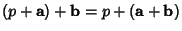, - 3. For any
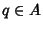, there Exists a unique Vector 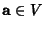such that 
.
, 
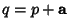. Note that (1) is implied by (2) and (3). Then is an affine space and is called the Coefficient Field.In an affine space, it is possible to fix a point and coordinate axis such that every point in the Space can berepresented as an 
-tuple of its coordinates. Every ordered pair of points and 
in an affine space is thenassociated with a Vector 
.
- Whitehead Manifold
- Whitehead's Theorem
- Whitney-Graustein Theorem
- Whitney-Mikhlin Extension Constants
- Whitney Singularity
- Whitney Sum
- Whitney Umbrella
- Whittaker Differential Equation
- Whittaker Function
- Whole Number
- Width (Partial Order)
- Width (Size)
- Wiedersehen Manifold
- Wieferich Prime
- Wielandt's Theorem
- Wiener Filter
- Wiener Function
- Wiener-Khintchine Theorem
- Wiener Measure
- Wiener Space
- Wigner 3j-Symbol
- Wigner 6j-Symbol
- Wigner 9j-Symbol
- Wigner-Eckart Theorem
- Wilbraham-Gibbs Constant