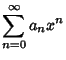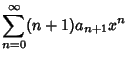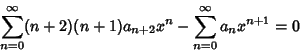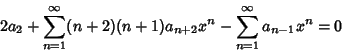| 释义 |
Airy Differential EquationSome authors define a general Airy differential equation as
 | (1) |
Specializing to the ``conventional'' Airy differential equation occurs by taking the Minus Sign and setting . Then plug (4) into . Then plug (4) into
 | (5) |
 | (6) |
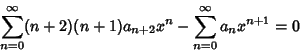 | (7) |
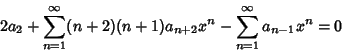 | (8) |
 | (9) |
 , each term must separately be 0. Therefore, , each term must separately be 0. Therefore,
Starting with the 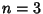 term and using the above Recurrence Relation, we obtain term and using the above Recurrence Relation, we obtain
 | (12) |
 | (13) |
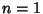 , 2, .... Now examine terms of the form , 2, .... Now examine terms of the form  . .
Again by Induction,
 | (17) |
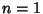 , 2, .... Finally, look at terms of the form , 2, .... Finally, look at terms of the form  , ,
By Induction,
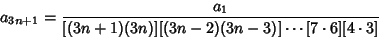 | (21) |
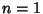 , 2, .... The general solution is therefore , 2, .... The general solution is therefore | | 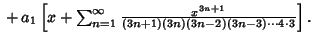 | | | (22) |
For a general 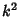 with a Minus Sign, equation (1) is with a Minus Sign, equation (1) is
 | (23) |
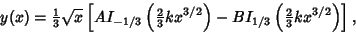 | (24) |
 is a Modified Bessel Function of the First Kind. This is usually expressed in terms of the AiryFunctions is a Modified Bessel Function of the First Kind. This is usually expressed in terms of the AiryFunctions  and and 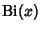
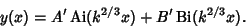 | (25) |
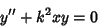 | (26) |
 | (27) |
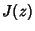 is a Bessel Function of the First Kind.See also Airy-Fock Functions, Airy Functions, Bessel Function of the First Kind, Modified BesselFunction of the First Kind is a Bessel Function of the First Kind.See also Airy-Fock Functions, Airy Functions, Bessel Function of the First Kind, Modified BesselFunction of the First Kind |