| 释义 |
K-FunctionAn extension of the  -function -function
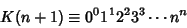 | (1) |
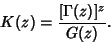 | (2) |
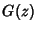 is the G-Function defined by is the G-Function defined by
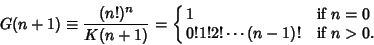 | (3) |
The  -function is given by the integral -function is given by the integral
 | (4) |
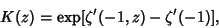 | (5) |
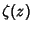 is the Riemann Zeta Function, is the Riemann Zeta Function, 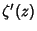 its Derivative, its Derivative, 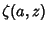 is theHurwitz Zeta Function, and is theHurwitz Zeta Function, and
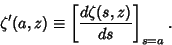 | (6) |
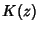 also has a Stirling-like series also has a Stirling-like series
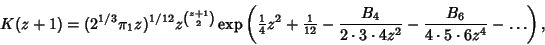 | (7) |
and 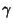 is the Euler-Mascheroni Constant (Gosper). is the Euler-Mascheroni Constant (Gosper).
The first few values of  for for 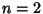 , 3, ... are 1, 4, 108, 27648, 86400000, 4031078400000, ... (Sloane's A002109). These numbers are called Hyperfactorials by Sloane and Plouffe (1995). , 3, ... are 1, 4, 108, 27648, 86400000, 4031078400000, ... (Sloane's A002109). These numbers are called Hyperfactorials by Sloane and Plouffe (1995). See also G-Function, Glaisher-Kinkelin Constant, Hyperfactorial, Stirling's Series
References
Sloane, N. J. A. SequenceA002109/M3706in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
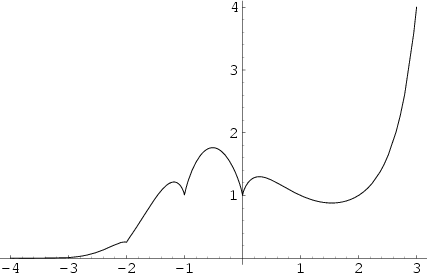
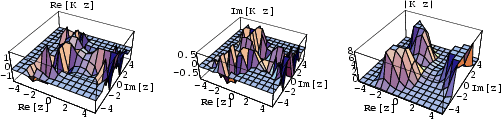
![]() -function
-function![]() -function is given by the integral
-function is given by the integral![]() for
for ![]() , 3, ... are 1, 4, 108, 27648, 86400000, 4031078400000, ... (Sloane's A002109). These numbers are called Hyperfactorials by Sloane and Plouffe (1995).
, 3, ... are 1, 4, 108, 27648, 86400000, 4031078400000, ... (Sloane's A002109). These numbers are called Hyperfactorials by Sloane and Plouffe (1995).