| 释义 |
Quadratic ResidueIf there is an Integer  such that such that
 | (1) |
 is said to be a quadratic residue (mod is said to be a quadratic residue (mod  ). If not, ). If not,  is said to be a quadratic nonresidue (mod is said to be a quadratic nonresidue (mod  ). Forexample, ). Forexample, 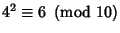 , so 6 is a quadratic residue (mod 10). The entire set of quadratic residues (mod 10) are given by1, 4, 5, 6, and 9, since , so 6 is a quadratic residue (mod 10). The entire set of quadratic residues (mod 10) are given by1, 4, 5, 6, and 9, since
making the numbers 2, 3, 7, and 8 the quadratic nonresidues (mod 10).
A list of quadratic residues for 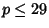 is given below (Sloane's A046071), with those numbers is given below (Sloane's A046071), with those numbers  not in the list being quadraticnonresidues of not in the list being quadraticnonresidues of  . .  | Quadratic Residues | | 1 | (none) | | 2 | 1 | | 3 | 1 | | 4 | 1 | | 5 | 1, 4 | | 6 | 1, 3, 4 | | 7 | 1, 2, 4 | | 8 | 1, 4 | | 9 | 1, 4, 7 | | 10 | 1, 4, 5, 6, 9 | | 11 | 1, 3, 4, 5, 9 | | 12 | 1, 4, 9 | | 13 | 1, 3, 4, 9, 10, 12 | | 14 | 1, 2, 4, 7, 8, 9, 11 | | 15 | 1, 4, 6, 9, 10 | | 16 | 1, 4, 9 | | 17 | 1, 2, 4, 8, 9, 13, 15, 16 | | 18 | 1, 4, 7, 9, 10, 13, 16 | | 19 | 1, 4, 5, 6, 7, 9, 11, 16, 17 | | 20 | 1, 4, 5, 9, 16 |
Given an Odd Prime  and an Integer and an Integer  , then the Legendre Symbol is given by , then the Legendre Symbol is given by
 | (2) |
 | (3) |
 is a quadratic residue (+) or nonresidue ( is a quadratic residue (+) or nonresidue ( ). This can be seen since if ). This can be seen since if  is a quadratic residue of is a quadratic residue of  ,then there exists a square ,then there exists a square  such that such that  , so , so
 | (4) |
 is congruent to 1 (mod is congruent to 1 (mod  ) by Fermat's Little Theorem. ) by Fermat's Little Theorem.  is given by is given by
 | (5) |
More generally, let  be a quadratic residue modulo an Odd Prime be a quadratic residue modulo an Odd Prime  . Choose . Choose  such that the Legendre Symbol such that the Legendre Symbol . Then defining . Then defining
gives
and a solution to the quadratic Congruence is
 | (11) |
The following table gives the Primes which have a given number  as a quadratic residue. as a quadratic residue.
Finding the Continued Fraction of a Square Root  and usingthe relationship and usingthe relationship
 | (12) |
 th Convergent th Convergent  gives gives
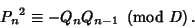 | (13) |
 is a quadratic residue of is a quadratic residue of 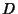 . But since . But since 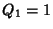 , ,  is a quadratic residue, as must be is a quadratic residue, as must be  .But since .But since  is a quadratic residue, so is is a quadratic residue, so is  , and we see that , and we see that  are all quadratic residues of are all quadratic residues of 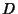 .This method is not guaranteed to produce all quadratic residues, but can often produce several small ones in the case oflarge .This method is not guaranteed to produce all quadratic residues, but can often produce several small ones in the case oflarge 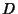 , enabling , enabling 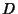 to be factored. to be factored.
The number of Squares 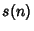 in in  is related to the number is related to the number  of quadraticresidues in of quadraticresidues in  by by
 | (14) |
 (Stangl 1996). Both (Stangl 1996). Both  and and  are Multiplicative Functions.See also Euler's Criterion, Multiplicative Function,Quadratic Reciprocity Theorem, Riemann Hypothesis are Multiplicative Functions.See also Euler's Criterion, Multiplicative Function,Quadratic Reciprocity Theorem, Riemann Hypothesis
References
Burton, D. M. Elementary Number Theory, 4th ed. New York: McGraw-Hill, p. 201, 1997.Courant, R. and Robbins, H. ``Quadratic Residues.'' §2.3 in Supplement to Ch. 1 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 38-40, 1996. Guy, R. K. ``Quadratic Residues. Schur's Conjecture'' and ``Patterns of Quadratic Residues.'' §F5 and F6 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 244-248, 1994. Niven, I. and Zuckerman, H. An Introduction to the Theory of Numbers, 4th ed. New York: Wiley, p. 84, 1980. Rosen, K. H. Ch. 9 in Elementary Number Theory and Its Applications, 3rd ed. Reading, MA: Addison-Wesley, 1993. Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 63-66, 1993. Sloane, N. J. A. Sequence A046071in ``The On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Stangl, W. D. ``Counting Squares in  .'' Math. Mag. 69, 285-289, 1996. .'' Math. Mag. 69, 285-289, 1996. Wagon, S. ``Quadratic Residues.'' §9.2 in Mathematica in Action. New York: W. H. Freeman, pp. 292-296, 1991. |
![]() such that
such that ![]() is given below (Sloane's A046071), with those numbers
is given below (Sloane's A046071), with those numbers ![]() not in the list being quadraticnonresidues of
not in the list being quadraticnonresidues of ![]() .
.![]() and an Integer
and an Integer ![]() , then the Legendre Symbol is given by
, then the Legendre Symbol is given by
![]() be a quadratic residue modulo an Odd Prime
be a quadratic residue modulo an Odd Prime ![]() . Choose
. Choose ![]() such that the Legendre Symbol
such that the Legendre Symbol![]() . Then defining
. Then defining![]() as a quadratic residue.
as a quadratic residue.![]() and usingthe relationship
and usingthe relationship ![]() in
in ![]() is related to the number
is related to the number ![]() of quadraticresidues in
of quadraticresidues in ![]() by
by![]() .'' Math. Mag. 69, 285-289, 1996.
.'' Math. Mag. 69, 285-289, 1996.