“Circle Lattice Points”的概念、定义、习题解题方法及翻译-数学辞典

单词

Circle Lattice Points

释义

Circle Lattice Points

For every Positive Integer , there exists a Circle which contains exactly lattice points in itsinterior. H. Steinhaus proved that for every Positive Integer , there exists a Circle of Area which contains exactly lattice points in its interior.

Schinzel's Theorem shows that for every Positive Integer , there exists a Circle in the Planehaving exactly Lattice Points on its Circumference. The theorem also explicitly identifiessuch ``Schinzel Circles'' as

(1)

Note, however, that these solutions do not necessarily have the smallest possible Radius. For example, while theSchinzel Circle centered at (1/3, 0) and with Radius 625/3 has nine lattice points on its Circumference, sodoes the Circle centered at (1/3, 0) with Radius 65/3.

Let be the smallest Integer Radius of a Circle centered at the Origin (0, 0) with Lattice Points. In order to find the number of lattice points of the Circle, it is onlynecessary to find the number in the first octant, i.e., those with , where is theFloor Function. Calling this , then for , , so . The multiplication byeight counts all octants, and the subtraction by four eliminates points on the axes which the multiplication counts twice. (Since is Irrational, the Midpoint of a are is never a Lattice Point.)

Gauss's Circle Problem asks for the number of lattice points within a Circle of Radius

(2)

Gauß

showed that

(3)

where

(4)

The number of lattice points on the Circumference of circles centered at (0, 0) with radii 0, 1, 2, ... are 1, 4, 4,4, 4, 12, 4, 4, 4, 4, 12, 4, 4, ... (Sloane's A046109). The following table gives the smallest Radius fora circle centered at (0, 0) having a given number of Lattice Points . Note that the high water markradii are always multiples of five.


1	0	108	1,105
4	1	132	40,625
12	5	140	21,125
20	25	156	203,125
28	125	180	5,525
36	65	196	274,625
44	3,125	252	27,625
52	15,625	300	71,825
60	325	324	32,045
68	390,625	420	359,125
76		540	160,225
84	1,625
92
100	4,225

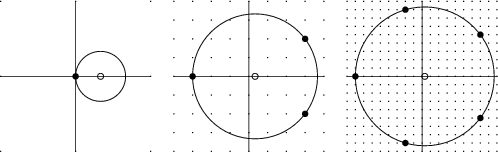
If the Circle is instead centered at (1/2, 0), then the Circles of Radii 1/2, 3/2,5/2, ... have 2, 2, 6, 2, 2, 2, 6, 6, 6, 2, 2, 2, 10, 2, ... (Sloane's A046110) on theirCircumferences. If the Circle is instead centered at (1/3, 0), then the number of lattice pointson the Circumference of the Circles of Radius 1/3, 2/3, 4/3, 5/3, 7/3, 8/3, ... are 1, 1, 1,3, 1, 1, 3, 1, 3, 1, 1, 3, 1, 3, 1, 1, 5, 3, ... (Sloane's A046111).

Let

: 1. be the Radius of the Circle centered at (0, 0) having lattice points on itsCircumference,
: 2. 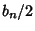be the Radius of the Circle centered at (1/2, 0) having lattice points on itsCircumference,
: 3. 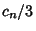be the Radius of Circle centered at (1/3, 0) having lattice points on itsCircumference.

Then the sequences

, and

are equal, with the exception that

and

.However, the sequences of smallest radii having the above numbers of lattice points are equal in the three cases and given by 1, 5, 25, 125, 65, 3125, 15625, 325, ... (Sloane's A046112).

Kulikowski's Theorem states that for every Positive Integer , there exists a 3-D Sphere which hasexactly Lattice Points on its surface. The Sphere is given by the equation

where

and

are the coordinates of the center of the so-called SchinzelCircle and

is its Radius (Honsberger 1973).

See also Circle, Circumference, Gauss's Circle Problem, Kulikowski's Theorem, Lattice Point, Schinzel Circle, Schinzel's Theorem

References

Honsberger, R. ``Circles, Squares, and Lattice Points.'' Ch. 11 in Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 117-127, 1973.

Kulikowski, T. ``Sur l'existence d'une sphère passant par un nombre donné aux coordonnées entières.'' L'Enseignement Math. Ser. 2 5, 89-90, 1959.

Schinzel, A. ``Sur l'existence d'un cercle passant par un nombre donné de points aux coordonnées entières.'' L'Enseignement Math. Ser. 2 4, 71-72, 1958.

Sierpinski, W. ``Sur quelques problèmes concernant les points aux coordonnées entières.'' L'Enseignement Math. Ser. 2 4, 25-31, 1958.

Sierpinski, W. ``Sur un problème de H. Steinhaus concernant les ensembles de points sur le plan.'' Fund. Math. 46, 191-194, 1959.

Sierpinski, W. A Selection of Problems in the Theory of Numbers. New York: Pergamon Press, 1964.

Weisstein, E. W. ``Circle Lattice Points.'' Mathematica notebook CircleLatticePoints.m.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。