“Quartic Curve”的概念、定义、习题解题方法及翻译-数学辞典

单词

Quartic Curve

释义

Quartic Curve

A general plane quartic curve is a curve of the form



	(1)

The incidence relations of the 28 bitangents of the general quartic curve can be put into a One-to-One correspondence withthe vertices of a particular Polytope in 7-D space (Coxeter 1928, Du Val 1931). This fact is essentially similar to thediscovery by Schoutte (1910) that the 27 Solomon's Seal Lines on a Cubic Surface can be connected with aPolytope in 6-D space (Du Val 1931). A similar but less complete relation exists between the tritangent planes of thecanonical curve of genus 4 and an 8-D Polytope (Du Val 1931).

The maximum number of Double Points for a nondegenerate quartic curve is three.

A quartic curve of the form

(2)

can be written

(3)

and so is Cubic in the coordinates

			(4)
			(5)

This transformation is a Birational Transformation.

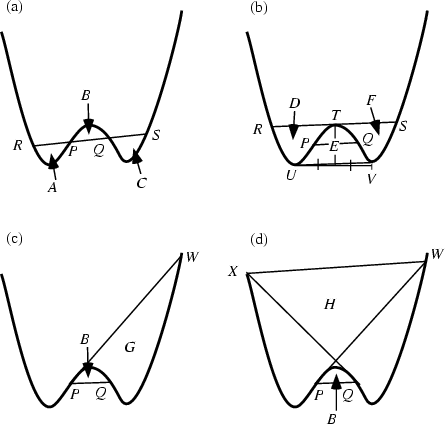
Let and be the Inflection Points and and the intersections of the line with the curve in Figure (a) above. Then

			(6)
			(7)

In Figure (b), let

be the double tangent, and

the point on the curve whose

coordinate is the average of the

coordinates of

and

. Then

and

			(8)
			(9)

In Figure (c), the tangent at

intersects the curve at

. Then

(10)

Finally, in Figure (d), the intersections of the tangents at

and

are

and

. Then

(11)

(Honsberger 1991).

See also Cubic Surface, Pear-Shaped Curve, Solomon's Seal Lines

References

Coxeter, H. S. M. ``The Pure Archimedean Polytopes in Six and Seven Dimensions.'' Proc. Cambridge Phil. Soc. 24, 7-9, 1928.

Du Val, P. ``On the Directrices of a Set of Points in a Plane.'' Proc. London Math. Soc. Ser. 2 35, 23-74, 1933.

Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 114-118, 1991.

Schoutte, P. H. ``On the Relation Between the Vertices of a Definite Sixdimensional Polytope and the Lines of a Cubic Surface.'' Proc. Roy. Akad. Acad. Amsterdam 13, 375-383, 1910.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。