Fontené Theorems
- 1. If the sides of the Pedal Triangle of a point
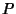 meet the corresponding sides of a Triangle
meet the corresponding sides of a Triangle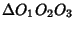 at
at 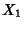 ,
, 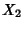 , and
, and  , respectively, then
, respectively, then  ,
, 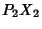 ,
, 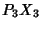 meet at a point
meet at a point  common to the Circles
common to the Circles  and
and  . In other words,
. In other words,  is one of the intersectionsof the Nine-Point Circle of
is one of the intersectionsof the Nine-Point Circle of  and the Pedal Circle of
and the Pedal Circle of 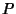 .
. - 2. If a point moves on a fixed line through the Circumcenter, then its Pedal Circle passesthrough a fixed point on the Nine-Point Circle.
- 3. The Pedal Circle of a point is tangent to the Nine-Point Circle Iff the point and itsIsogonal Conjugate lie on a Line through the Orthocenter. Feuerbach's Theorem is a special case of this theorem.
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 245-247, 1929.
- Slothouber-Graatsma Puzzle
- Slutzky-Yule Effect
- Sluze Pearls
- Smale-Hirsch Theorem
- Smale Horseshoe Map
- Small Cubicuboctahedron
- Small Ditrigonal Dodecacronic Hexecontahedron
- Small Ditrigonal Dodecicosidodecahedron
- Small Ditrigonal Icosidodecahedron
- Small Dodecacronic Hexecontahedron
- Small Dodecahemicosacron
- Small Dodecahemicosahedron
- Small Dodecahemidodecacron
- Small Dodecahemidodecahedron
- Small Dodecicosacron
- Small Dodecicosahedron
- Small Dodecicosidodecahedron
- Small Hexacronic Icositetrahedron
- Small Hexagonal Hexecontahedron
- Small Hexagrammic Hexecontahedron
- Small Icosacronic Hexecontahedron
- Small Icosicosidodecahedron
- Small Icosihemidodecacron
- Small Icosihemidodecahedron
- Small Inverted Retrosnub Icosicosidodecahedron