Alexander's Horned Sphere

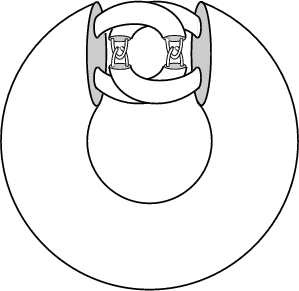
The above solid, composed of a countable Union of Compact Sets, is called Alexander's hornedsphere. It is Homeomorphic with the Ball , and its boundary is therefore a Sphere. It istherefore an example of a wild embedding in . The outer complement of the solid is not Simply Connected,and its fundamental Group is not finitely generated. Furthermore, the set of nonlocally flat (``bad'') points ofAlexander's horned sphere is a Cantor Set.

The complement in of the bad points for Alexander's horned sphere is Simply Connected, making itinequivalent to Antoine's Horned Sphere. Alexander's horned sphere has an uncountable infinity of WildPoints, which are the limits of the sequences of the horned sphere's branch points (roughly, the ``ends'' ofthe horns), since any Neighborhood of a limit contains a horned complex.

A humorous drawing by Simon Frazer (Guy 1983, Schroeder 1991, Albers 1994) depicts mathematician John H. Conway with Alexander's horned sphere growing from his head.

References

Albers, D. J. Illustration accompanying ``The Game of `Life'.'' Math Horizons, p. 9, Spring 1994.

Guy, R. ``Conway's Prime Producing Machine.'' Math. Mag. 56, 26-33, 1983.

Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 80-81, 1976.

Schroeder, M. Fractals, Chaos, Power Law: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 58, 1991.

• Infinitesimal Analysis
• Infinitesimal Matrix Change
• Infinitesimal Rotation
• Infinitive Sequence
• Infinitude of Primes
• Infinity
• Inflection Point
• Information Dimension
• Information Entropy
• Information Theory
• Initial Value Problem
• Injection
• Injective
• Injective Patch
• Inner Automorphism Group
• Inner Product
• Inner Product Space
• Inradius
• Inscribed
• Inscribed Angle
• Inside-Outside Theorem
• Insphere
• Instrument Function
• Insufficient Reason Principle
• Int