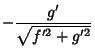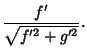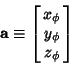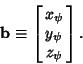| 释义 |
Normal VectorThe normal to a Plane specified by
 | (1) |
 | (2) |
 on a surface on a surface 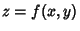 is is
 | (3) |
In the Plane, the unit normal vector is defined by
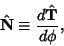 | (4) |
 is the unit Tangent Vector and is the unit Tangent Vector and 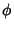 is the polar angle. Given a unit Tangent Vector is the polar angle. Given a unit Tangent Vector
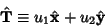 | (5) |
 , the normal is , the normal is
 | (6) |
 , the normal vector relative to the point , the normal vector relative to the point  istherefore given by istherefore given by
To actually place the vector normal to the curve, it must be displaced by  . .
In 3-D Space, the unit normal is
 | (9) |
 is the Curvature. Given a 3-D surface is the Curvature. Given a 3-D surface 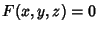 , ,
 | (10) |
define the Vectors
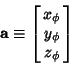 | (14) |
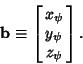 | (15) |
 | (16) |
 be the discriminant of the Metric Tensor. Then be the discriminant of the Metric Tensor. Then
 | (17) |
References
Gray, A. ``Tangent and Normal Lines to Plane Curves.'' §5.5 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 85-90, 1993. |