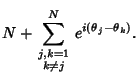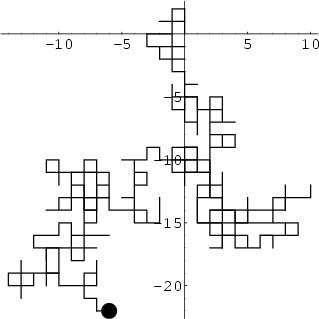| 释义 |
Random Walk--2-DIn a Plane, consider a sum of  2-D Vectors with random orientations. Use Phasornotation, and let the phase of each Vector be Random. Assume 2-D Vectors with random orientations. Use Phasornotation, and let the phase of each Vector be Random. Assume  unit steps are takenin an arbitrary direction (i.e., with the angle unit steps are takenin an arbitrary direction (i.e., with the angle 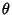 uniformly distributed in uniformly distributed in  and not on aLattice), as illustrated above. The position and not on aLattice), as illustrated above. The position  in the Complex Plane after in the Complex Plane after 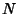 steps is then given by steps is then given by
 | (1) |
Therefore,
 | (3) |
 and and 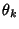 are Random Variables with identical Means of zero, and their difference is also a random variable. Averaging over thisdistribution, which has equally likely Positive and Negative values yields an expectation value of 0, so are Random Variables with identical Means of zero, and their difference is also a random variable. Averaging over thisdistribution, which has equally likely Positive and Negative values yields an expectation value of 0, so
 | (4) |
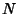 unit steps is therefore unit steps is therefore
 | (5) |
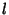 , this becomes , this becomes
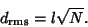 | (6) |

 | (7) |
Amazingly, it has been proven that on a 2-D Lattice, a random walk has unity probability of reaching any point(including the starting point) as the number of steps approaches Infinity. See also Pólya's Random Walk Constants, Random Walk--1-D, Random Walk--3-D |

![]() 2-D Vectors with random orientations. Use Phasornotation, and let the phase of each Vector be Random. Assume
2-D Vectors with random orientations. Use Phasornotation, and let the phase of each Vector be Random. Assume ![]() unit steps are takenin an arbitrary direction (i.e., with the angle
unit steps are takenin an arbitrary direction (i.e., with the angle ![]() uniformly distributed in
uniformly distributed in ![]() and not on aLattice), as illustrated above. The position
and not on aLattice), as illustrated above. The position ![]() in the Complex Plane after
in the Complex Plane after ![]() steps is then given by
steps is then given by