| 释义 |
Glaisher-Kinkelin ConstantN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Define
where  is the G-Function and is the G-Function and  is the K-Function. Then is the K-Function. Then
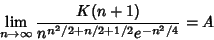 | (3) |
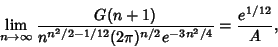 | (4) |
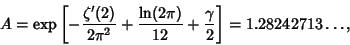 | (5) |
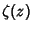 is the Riemann Zeta Function, is the Riemann Zeta Function,  is Pi, and is Pi, and 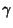 is the Euler-Mascheroni Constant (Kinkelin 1860, Glaisher 1877, 1878, 1893, 1894). Glaisher (1877) also obtained is the Euler-Mascheroni Constant (Kinkelin 1860, Glaisher 1877, 1878, 1893, 1894). Glaisher (1877) also obtained
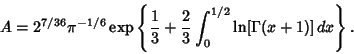 | (6) |
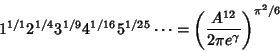 | (7) |
 | (8) |
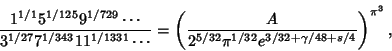 | (9) |
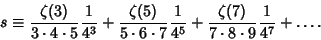 | (10) |
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/glshkn/glshkn.htmlGlaisher, J. W. L. ``On a Numerical Continued Product.'' Messenger Math. 6, 71-76, 1877. Glaisher, J. W. L. ``On the Product 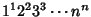 .'' Messenger Math. 7, 43-47, 1878. .'' Messenger Math. 7, 43-47, 1878. Glaisher, J. W. L. ``On Certain Numerical Products.'' Messenger Math. 23, 145-175, 1893. Glaisher, J. W. L. ``On the Constant which Occurs in the Formula for 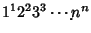 .'' Messenger Math. 24, 1-16, 1894. .'' Messenger Math. 24, 1-16, 1894. Kinkelin. ``Über eine mit der Gammafunktion verwandte Transcendente und deren Anwendung auf die Integralrechnung.'' J. Reine Angew. Math. 57, 122-158, 1860. |
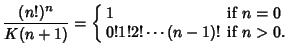
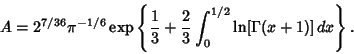
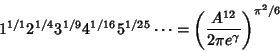

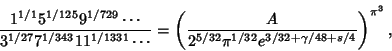
![]() .'' Messenger Math. 7, 43-47, 1878.
.'' Messenger Math. 7, 43-47, 1878.![]() .'' Messenger Math. 24, 1-16, 1894.
.'' Messenger Math. 24, 1-16, 1894.