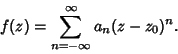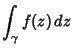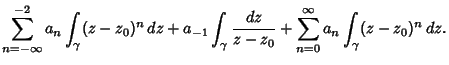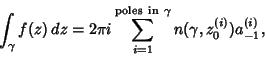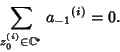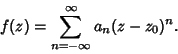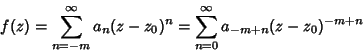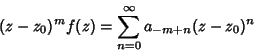| 释义 |
Residue Theorem (Complex Analysis)Given a complex function  , consider the Laurent Series , consider the Laurent Series
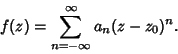 | (1) |
 encircling encircling 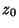 , ,
The Cauchy Integral Theorem requires that the first and last terms vanish, so we have
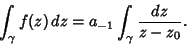 | (3) |
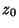 ) using the Cauchy Integral Formula, ) using the Cauchy Integral Formula,
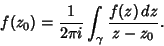 | (4) |
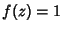 , in which case it is also true that , in which case it is also true that 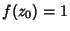 , so , so
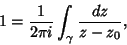 | (5) |
 | (6) |
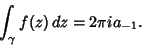 | (7) |
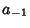 is known as the Residue of is known as the Residue of  at at 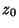 . Generalizing to acurve passing through multiple poles, (7) becomes . Generalizing to acurve passing through multiple poles, (7) becomes
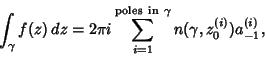 | (8) |
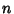 is the Winding Number and the is the Winding Number and the  superscript denotes the quantitycorresponding to Pole superscript denotes the quantitycorresponding to Pole 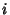 . .
If the path does not completely encircle the Residue, take the Cauchy Principal Value to obtain
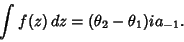 | (9) |
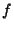 has only Isolated Singularities, then has only Isolated Singularities, then
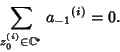 | (10) |
The residues may be found without explicitly expanding into a Laurent Series as follows:
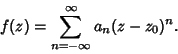 | (11) |
 has a Pole of order has a Pole of order 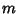 at at 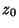 , then , then 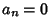 for for  and and 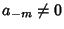 . Therefore, . Therefore,
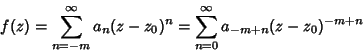 | (12) |
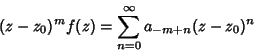 | (13) |
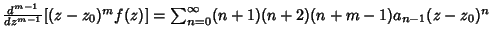 | | 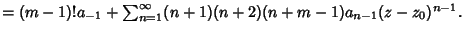 | (16) |
So
 | (17) |
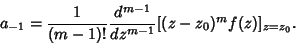 | (18) |
This amazing theorem says that the value of a Contour Integral in the Complex Plane depends only onthe properties of a few special points inside the contour. See also Cauchy Integral Formula, Cauchy Integral Theorem, Contour Integral, Laurent Series,Pole, Residue (Complex Analysis) |
![]() , consider the Laurent Series
, consider the Laurent Series