| 释义 |
Riemann TensorA Tensor sometimes known as the Riemann-Christoffel Tensor. Let
 | (1) |
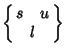 is a Christoffel Symbol of the Second Kind. Then is a Christoffel Symbol of the Second Kind. Then
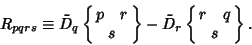 | (2) |
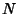 -D, -D, 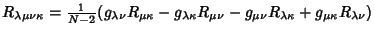 | |  | (3) |
Here,  is the Ricci Tensor, is the Ricci Tensor, 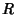 is the Curvature Scalar, and is the Curvature Scalar, and  is theWeyl Tensor. In terms of the Jacobi Tensor is theWeyl Tensor. In terms of the Jacobi Tensor  , ,
 | (4) |
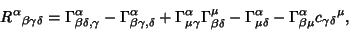 | (5) |
 are Connection Coefficients and are Connection Coefficients and  are CommutationCoefficients. The number of independent coordinates in are CommutationCoefficients. The number of independent coordinates in 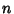 -D is -D is
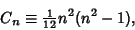 | (6) |
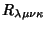 and and 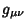 is is
 | (7) |
 .See also Bianchi Identities, Christoffel Symbol of the Second Kind, Commutation Coefficient,Connection Coefficient, Curvature Scalar, Gaussian Curvature, Jacobi Tensor, PetrovNotation, Ricci Tensor, Weyl Tensor .See also Bianchi Identities, Christoffel Symbol of the Second Kind, Commutation Coefficient,Connection Coefficient, Curvature Scalar, Gaussian Curvature, Jacobi Tensor, PetrovNotation, Ricci Tensor, Weyl Tensor |

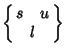 is a Christoffel Symbol of the Second Kind. Then
is a Christoffel Symbol of the Second Kind. Then