“Ring”的概念、定义、习题解题方法及翻译-数学辞典

单词

Ring

释义

Ring

A ring is a set together with two Binary Operators satisfying the following conditions:

: 1. Additive associativity: For all , ,
: 2. Additive commutativity: For all , ,
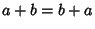: 3. Additive identity: There exists an element such that for all , ,
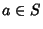: 4. Additive inverse: For every 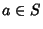there exists 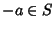such that ,
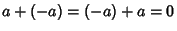: 5. Multiplicative associativity: For all , ,
: 6. Left and right distributivity: For all , 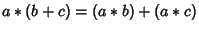and .

A ring is therefore an Abelian Group under addition and a Semigroup under multiplication. A ring must containat least one element, but need not contain a multiplicative identity or be commutative. The number of finite rings of

elementsfor

, 2, ..., are 1, 2, 2, 11, 2, 4, 2, 52, 11, 4, 2, 22, 2, 4, 4, ... (Sloane's A027623and A037234; Fletcher 1980).In general, the number of rings of order

for

an Odd Prime is

and 52 for

(Ballieu 1947, Gilmer and Mott 1973).

A ring with a multiplicative identity is sometimes called a Unit Ring. Fraenkel (1914) gave the first abstractdefinition of the ring, although this work did not have much impact.

A ring that is Commutative under multiplication, has a unit element, and has no divisors of zero is called anIntegral Domain. A ring which is also a Commutative multiplication group is called a Field. The simplestrings are the Integers , Polynomials and in oneand two variables, and Square Real Matrices.

Rings which have been investigated and found to be of interest are usually named after one or more of their investigators. This practice unfortunately leads to names which give very little insight into the relevant properties of the associatedrings.

See also Abelian Group, Artinian Ring, Chow Ring, Dedekind Ring, Division Algebra,Field, Gorenstein Ring, Group, Group Ring, Ideal, Integral Domain, Module,Nilpotent Element, Noetherian Ring, Number Field, Prime Ring, Prüfer Ring, Quotient Ring, Regular Ring, Ringoid, Semiprime Ring, Semiring, SemisimpleRing, Simple Ring, Unit Ring, Zero Divisor

References

Ballieu, R. ``Anneaux finis; systèmes hypercomplexes de rang trois sur un corps commutatif.'' Ann. Soc. Sci. Bruxelles. Sér. I 61, 222-227, 1947.

Fletcher, C. R. ``Rings of Small Order.'' Math. Gaz. 64, 9-22, 1980.

Fraenkel, A. ``Über die Teiler der Null und die Zerlegung von Ringen.'' J. Reine Angew. Math. 145, 139-176, 1914.

Gilmer, R. and Mott, J. ``Associative Rings of Order .'' Proc. Japan Acad. 49, 795-799, 1973.

Kleiner, I. ``The Genesis of the Abstract Ring Concept.'' Amer. Math. Monthly 103, 417-424, 1996.

Sloane, N. J. A.A027623 andA037234 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html.

van der Waerden, B. L. A History of Algebra. New York: Springer-Verlag, 1985.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。