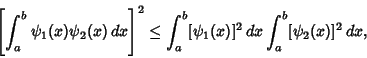| 释义 |
Schwarz's Inequality
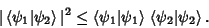 | (1) |
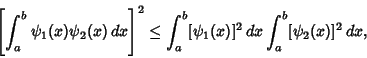 | (2) |
 with with 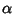 a constant. To derive, let a constant. To derive, let  be aComplex function and be aComplex function and  a Complex constant such that a Complex constant such that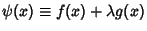 for some for some 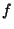 and and 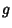 . Since . Since 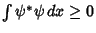 , ,
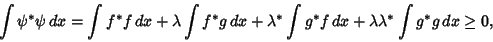 | (3) |
 . Set . Set
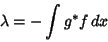 | (4) |
 | (5) |
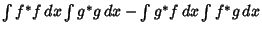 | | 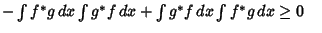 | (6) |
 | (7) |
 | (8) |
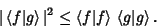 | (9) |
ReferencesAbramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 11, 1972.Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 527-529, 1985.
|