| 释义 |
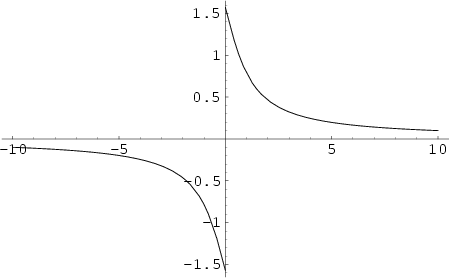
Inverse CotangentThe function  , also denoted arccot( , also denoted arccot(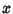 ), where ), where 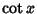 is the Cotangent and the superscript is the Cotangent and the superscript 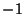 denotes anInverse Function and not the multiplicative inverse. The Maclaurin Series is given by denotes anInverse Function and not the multiplicative inverse. The Maclaurin Series is given by
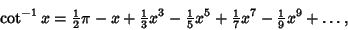 | (1) |
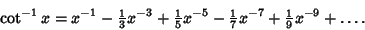 | (2) |
 derived the Infinite series derived the Infinite series
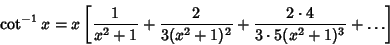 | (3) |
The inverse cotangent satisfies
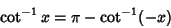 | (4) |
 , and , and
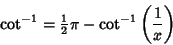 | (5) |
 . The inverse cotangent is given in terms of other inverse trigonometric functions by . The inverse cotangent is given in terms of other inverse trigonometric functions by
for Positive or Negative 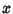 , and , and
for  . .
A number
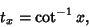 | (13) |
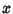 is an Integer or Rational Number, is sometimes called a Gregory Number. Lehmer (1938a) showed that is an Integer or Rational Number, is sometimes called a Gregory Number. Lehmer (1938a) showed that can be expressed as a finite sum of inverse cotangents of Integer arguments can be expressed as a finite sum of inverse cotangents of Integer arguments
 | (14) |
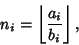 | (15) |
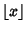 the Floor Function, and the Floor Function, and
with 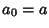 and and 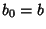 , and where the recurrence is continued until , and where the recurrence is continued until 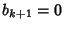 . If an Inverse Tangent sum is writtenas . If an Inverse Tangent sum is writtenas
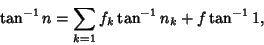 | (18) |
 | (19) |
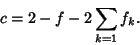 | (20) |
An interesting inverse cotangent identity attributed to Charles Dodgson (Lewis Carroll) by Lehmer (1938b; Bromwich 1965,Castellanos 1988ab) is
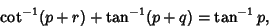 | (21) |
 | (22) |
Other inverse cotangent identities include
 | (23) |
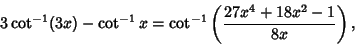 | (24) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Inverse Circular Functions.'' §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.Bennett, A. A. ``The Four Term Diophantine Arccotangent Relation.'' Ann. Math. 27, 21-24, 1926. Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987. Bromwich, T. J. I. and MacRobert, T. M. An Introduction to the Theory of Infinite Series, 3rd ed. New York: Chelsea, 1991. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988a. Castellanos, D. ``The Ubiquitous Pi. Part II.'' Math. Mag. 61, 148-163, 1988b. Lehmer, D. H. ``A Cotangent Analogue of Continued Fractions.'' Duke Math. J. 4, 323-340, 1938a. Lehmer, D. H. ``On Arccotangent Relations for  .'' Amer. Math. Monthly 45, 657-664, 1938b. .'' Amer. Math. Monthly 45, 657-664, 1938b.  Weisstein, E. W. ``Arccotangent Series.'' Mathematica notebook CotSeries.m. Weisstein, E. W. ``Arccotangent Series.'' Mathematica notebook CotSeries.m.
Wetherfield, M. ``The Enhancement of Machin's Formula by Todd's Process.'' Math. Gaz., 333-344, July 1996.
|

![]() , also denoted arccot(
, also denoted arccot(![]() ), where
), where ![]() is the Cotangent and the superscript
is the Cotangent and the superscript ![]() denotes anInverse Function and not the multiplicative inverse. The Maclaurin Series is given by
denotes anInverse Function and not the multiplicative inverse. The Maclaurin Series is given by
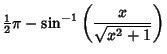
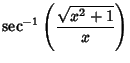

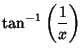

![]() .'' Amer. Math. Monthly 45, 657-664, 1938b.
.'' Amer. Math. Monthly 45, 657-664, 1938b.![]() Weisstein, E. W. ``Arccotangent Series.'' Mathematica notebook CotSeries.m.
Weisstein, E. W. ``Arccotangent Series.'' Mathematica notebook CotSeries.m.