“Alternating Permutation”的概念、定义、习题解题方法及翻译-数学辞典

单词

Alternating Permutation

释义

Alternating Permutation

An arrangement of the elements , ..., such that no element has a magnitude between and is called an alternating (or Zigzag) permutation. The determination of the numberof alternating permutations for the set of the first Integers is known asAndré's Problem. An example of an alternating permutation is (1, 3, 2, 5, 4).

As many alternating permutations among elements begin by rising as by falling. The magnitude of thes does not matter; only the number of them. Let the number of alternating permutations be given by . Thisquantity can then be computed from

(1)

where

and

pass through all Integral numbers such that

(2)

, and

(3)

The numbers

are sometimes called the Euler Zigzag Numbers, and the first few are givenby 1, 1, 1, 2, 5, 16, 61, 272, ... (Sloane's A000111). The Odd-numbered

s are called Euler Numbers, Secant Numbers, or Zig Numbers, and the Even-numbered ones aresometimes called Tangent Numbers or Zag Numbers.

Curiously enough, the Secant and Tangent Maclaurin Series can be written in terms of the s as

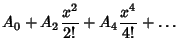			(4)
			(5)

or combining them,

(6)

See also Entringer Number, Euler Number, Euler Zigzag Number, Secant Number, Seidel-Entringer-Arnold Triangle, Tangent Number

References

André, D. ``Developments de et .'' C. R. Acad. Sci. Paris 88, 965-967, 1879.

André, D. ``Memoire sur les permutations alternées.'' J. Math. 7, 167-184, 1881.

Arnold, V. I. ``Bernoulli-Euler Updown Numbers Associated with Function Singularities, Their Combinatorics and Arithmetics.'' Duke Math. J. 63, 537-555, 1991.

Arnold, V. I. ``Snake Calculus and Combinatorics of Bernoulli, Euler, and Springer Numbers for Coxeter Groups.'' Russian Math. Surveys 47, 3-45, 1992.

Bauslaugh, B. and Ruskey, F. ``Generating Alternating Permutations Lexicographically.'' BIT 30, 17-26, 1990.

Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 110-111, 1996.

Dörrie, H. ``André's Deviation of the Secant and Tangent Series.'' §16 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 64-69, 1965.

Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 69-75, 1985.

Knuth, D. E. and Buckholtz, T. J. ``Computation of Tangent, Euler, and Bernoulli Numbers.'' Math. Comput. 21, 663-688, 1967.

Millar, J.; Sloane, N. J. A.; and Young, N. E. ``A New Operation on Sequences: The Boustrophedon Transform.'' J. Combin. Th. Ser. A 76, 44-54, 1996.

Ruskey, F. ``Information of Alternating Permutations.'' http://sue.csc.uvic.ca/~cos/inf/perm/Alternating.html.

Sloane, N. J. A. SequenceA000111/M1492in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。