| 释义 |
Associative AlgebraIn simple terms, let  , ,  , and , and 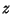 be members of an Algebra. Then the Algebra is said to be associativeif be members of an Algebra. Then the Algebra is said to be associativeif
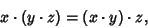 | (1) |
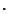 denotes Multiplication. More formally, let denotes Multiplication. More formally, let  denote an denote an  -algebra, so that -algebra, so that  is aVector Space over is aVector Space over  and and
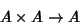 | (2) |
 | (3) |
 is said to be is said to be  -associative if there exists an -associative if there exists an  -D Subspace -D Subspace  of of  such that such that
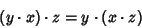 | (4) |
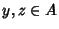 and and  . Here, Vector Multiplication . Here, Vector Multiplication 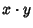 is assumed to be Bilinear.An is assumed to be Bilinear.An 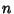 -D -D 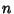 -associative Algebra is simply said to be ``associative.''See also Associative -associative Algebra is simply said to be ``associative.''See also Associative
References
Finch, S. ``Zero Structures in Real Algebras.'' http://www.mathsoft.com/asolve/zerodiv/zerodiv.html.
|
![]() ,
, ![]() , and
, and ![]() be members of an Algebra. Then the Algebra is said to be associativeif
be members of an Algebra. Then the Algebra is said to be associativeif