| 释义 |
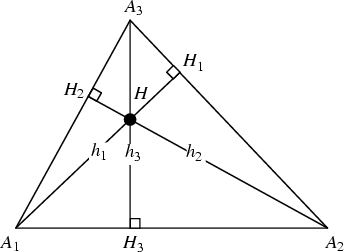
AltitudeThe altitudes of a Triangle are the Cevians 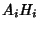 which are Perpendicular to the Legs which are Perpendicular to the Legs 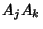 opposite opposite 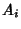 . They have lengths . They have lengths 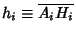 given by given by
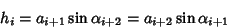 | (1) |
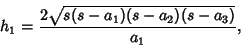 | (2) |
 is the Semiperimeter of is the Semiperimeter of  and and  . Another interesting Formula is . Another interesting Formula is
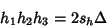 | (3) |
 is the Area of the Triangle is the Area of the Triangle  and and  is theSemiperimeter of the altitude triangle is theSemiperimeter of the altitude triangle  . The three altitudes of any Triangle areConcurrent at the Orthocenter . The three altitudes of any Triangle areConcurrent at the Orthocenter 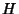 . This fundamental fact did not appear anywhere inEuclid's . This fundamental fact did not appear anywhere inEuclid's  Elements">Elements. Elements">Elements.
Other formulas satisfied by the altitude include
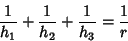 | (4) |
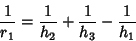 | (5) |
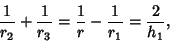 | (6) |
 is the Inradius and is the Inradius and 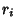 are the Exradii (Johnson 1929, p. 189). In addition, are the Exradii (Johnson 1929, p. 189). In addition,
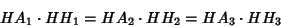 | (7) |
 | (8) |
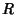 is the Circumradius. is the Circumradius.
The points  , , 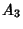 , , 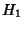 , and , and 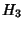 (and their permutations with respect to indices) all lie on a Circle, asdo the points (and their permutations with respect to indices) all lie on a Circle, asdo the points 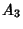 , , 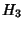 , , 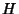 , and , and 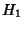 (and their permutations with respect to indices). Triangles (and their permutations with respect to indices). Triangles and and 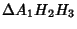 are inversely similar. are inversely similar.
The triangle  has the minimum Perimeter of any Triangle inscribed in a given Acute Triangle(Johnson 1929, pp. 161-165). The Perimeter of has the minimum Perimeter of any Triangle inscribed in a given Acute Triangle(Johnson 1929, pp. 161-165). The Perimeter of  is is 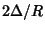 (Johnson 1929, p. 191). Additionalproperties involving the Feet of the altitudes are given by Johnson (1929, pp. 261-262). (Johnson 1929, p. 191). Additionalproperties involving the Feet of the altitudes are given by Johnson (1929, pp. 261-262). See also Cevian, Foot, Orthocenter, Perpendicular, Perpendicular Foot
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 9 and 36-40, 1967.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929. |
![]() which are Perpendicular to the Legs
which are Perpendicular to the Legs ![]() opposite
opposite ![]() . They have lengths
. They have lengths ![]() given by
given by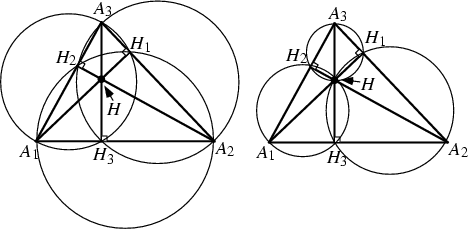
![]() ,
, ![]() ,
, ![]() , and
, and ![]() (and their permutations with respect to indices) all lie on a Circle, asdo the points
(and their permutations with respect to indices) all lie on a Circle, asdo the points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (and their permutations with respect to indices). Triangles
(and their permutations with respect to indices). Triangles![]() and
and ![]() are inversely similar.
are inversely similar. ![]() has the minimum Perimeter of any Triangle inscribed in a given Acute Triangle(Johnson 1929, pp. 161-165). The Perimeter of
has the minimum Perimeter of any Triangle inscribed in a given Acute Triangle(Johnson 1929, pp. 161-165). The Perimeter of ![]() is
is ![]() (Johnson 1929, p. 191). Additionalproperties involving the Feet of the altitudes are given by Johnson (1929, pp. 261-262).
(Johnson 1929, p. 191). Additionalproperties involving the Feet of the altitudes are given by Johnson (1929, pp. 261-262).