Doob's Theorem
A theorem proved by Doob (1942) which states that any random process which is both Gaussian and Markov has the following forms for its correlation function,spectral density, and probability densities:
 |  |  | (1) |
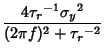 | |  | (2) |
 | |  | (3) |
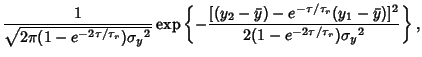 | |  | (4) |
where
is the Mean, 
the Standard Deviation, and 
the relaxation time.
References
Doob, J. L. ``Topics in the Theory of Markov Chains.'' Trans. Amer. Math. Soc. 52, 37-64, 1942.
- Gyroelongated Cupola
- Gyroelongated Dipyramid
- Gyroelongated Pentagonal Bicupola
- Gyroelongated Pentagonal Birotunda
- Gyroelongated Pentagonal Cupola
- Gyroelongated Pentagonal Cupolarotunda
- Gyroelongated Pentagonal Pyramid
- Gyroelongated Pentagonal Rotunda
- Gyroelongated Pyramid
- Gyroelongated Rotunda
- Gyroelongated Square Bicupola
- Gyroelongated Square Cupola
- Gyroelongated Square Dipyramid
- Gyroelongated Square Pyramid
- Gyroelongated Triangular Bicupola
- Gyroelongated Triangular Cupola
- Gårding's Inequality
- Göbel's Sequence
- Gödel Number
- Gödel's Completeness Theorem
- Gödel's Incompleteness Theorem
- Haar Function
- Haar Integral
- Haar Measure
- Haar Transform