| 释义 |
Apéry's ConstantN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Apéry's constant is defined by
 | (1) |
 is the Riemann Zeta Function. Apéry (1979) proved that is the Riemann Zeta Function. Apéry (1979) proved that  isIrrational, although it is not known if it is Transcendental. TheContinued Fraction for isIrrational, although it is not known if it is Transcendental. TheContinued Fraction for  is [1, 4, 1, 18, 1, 1, 1, 4, 1, ...] (Sloane's A013631). The positions at which thenumbers 1, 2, ... occur in the continued fraction are 1, 12, 25, 2, 64, 27, 17, 140, 10, ... (Sloane's A033165). is [1, 4, 1, 18, 1, 1, 1, 4, 1, ...] (Sloane's A013631). The positions at which thenumbers 1, 2, ... occur in the continued fraction are 1, 12, 25, 2, 64, 27, 17, 140, 10, ... (Sloane's A033165).
Sums related to  are are
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
 is the Dirichlet Lambda Function. The above equations are special cases of a general result due toRamanujan is the Dirichlet Lambda Function. The above equations are special cases of a general result due toRamanujan  (Berndt 1985). Apéry's proof relied on showing that the sum (Berndt 1985). Apéry's proof relied on showing that the sum
 | (7) |
 is a Binomial Coefficient, satisfies the Recurrence Relation is a Binomial Coefficient, satisfies the Recurrence Relation
 | (8) |
Apéry's constant is also given by
 | (9) |
 is a Stirling Number of the First Kind. This can be rewritten as is a Stirling Number of the First Kind. This can be rewritten as
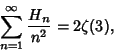 | (10) |
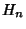 is the is the 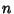 th Harmonic Number. Yet another expression for th Harmonic Number. Yet another expression for  is is
 | (11) |
Integrals for  include include
Gosper (1990) gave
 | (14) |
 | (15) |
 with with
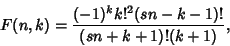 | (16) |
 to obtain to obtain
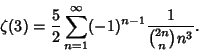 | (17) |
 , ,
 | (18) |
 , ,
 | (19) |
 for for  and 2 are and 2 are
 | (20) |
 | (21) |
 as the Matrix Product as the Matrix Product
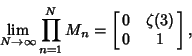 | (22) |
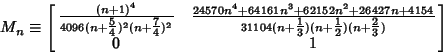 | (23) |
which gives 12 bits per term. The first few terms are
which gives
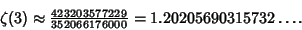 | (27) |
Given three Integers chosen at random, the probability that no common factor will divide them all is
 | (28) |
B. Haible and T. Papanikolaou computed  to 1,000,000 Digits using a Wilf-ZeilbergerPair identity with to 1,000,000 Digits using a Wilf-ZeilbergerPair identity with
 | (29) |
 , and , and 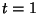 , giving the rapidly converging , giving the rapidly converging
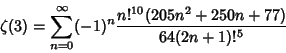 | (30) |
References
Amdeberhan, T. ``Faster and Faster Convergent Series for  .'' Electronic J. Combinatorics 3, R13 1-2, 1996.http://www.combinatorics.org/Volume_3/volume3.html#R13. .'' Electronic J. Combinatorics 3, R13 1-2, 1996.http://www.combinatorics.org/Volume_3/volume3.html#R13.Amdeberhan, T. and Zeilberger, D. ``Hypergeometric Series Acceleration via the WZ Method.'' Electronic J. Combinatorics 4, No. 2, R3, 1-3, 1997.http://www.combinatorics.org/Volume_4/wilftoc.html#R03. Also available at http://www.math.temple.edu/~zeilberg/mamarim/mamarimhtml/accel.html. Apéry, R. ``Irrationalité de  et et  .'' Astérisque 61, 11-13, 1979. .'' Astérisque 61, 11-13, 1979. Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, 1985. Beukers, F. ``A Note on the Irrationality of  .'' Bull. London Math. Soc. 11, 268-272, 1979. .'' Bull. London Math. Soc. 11, 268-272, 1979. Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987. Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988. Conway, J. H. and Guy, R. K. ``The Great Enigma.'' In The Book of Numbers. New York: Springer-Verlag, pp. 261-262, 1996. Ewell, J. A. ``A New Series Representation for  .'' Amer. Math. Monthly 97, 219-220, 1990. .'' Amer. Math. Monthly 97, 219-220, 1990. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/apery/apery.html Gosper, R. W. ``Strip Mining in the Abandoned Orefields of Nineteenth Century Mathematics.'' In Computers in Mathematics (Ed. D. V. Chudnovsky and R. D. Jenks). New York: Marcel Dekker, 1990. Haible, B. and Papanikolaou, T. ``Fast Multiprecision Evaluation of Series of Rational Numbers.'' Technical Report TI-97-7. Darmstadt, Germany: Darmstadt University of Technology, Apr. 1997. Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 36, 1983. Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computationof Constants.'' http://www.lacim.uqam.ca/pi/records.html. Sloane, N. J. A.A013631,A033165, andA002117/M0020in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. van der Poorten, A. ``A Proof that Euler Missed... Apéry's Proof of the Irrationality of  .'' Math. Intel. 1, 196-203, 1979. .'' Math. Intel. 1, 196-203, 1979. Zeilberger, D. ``The Method of Creative Telescoping.'' J. Symb. Comput. 11, 195-204, 1991. |
![]() are
are






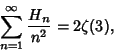

![]() include
include


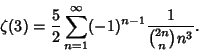


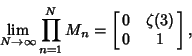
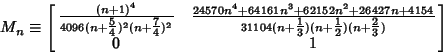
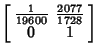


![]() to 1,000,000 Digits using a Wilf-ZeilbergerPair identity with
to 1,000,000 Digits using a Wilf-ZeilbergerPair identity with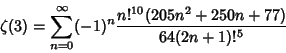
![]() .'' Electronic J. Combinatorics 3, R13 1-2, 1996.http://www.combinatorics.org/Volume_3/volume3.html#R13.
.'' Electronic J. Combinatorics 3, R13 1-2, 1996.http://www.combinatorics.org/Volume_3/volume3.html#R13.![]() et
et ![]() .'' Astérisque 61, 11-13, 1979.
.'' Astérisque 61, 11-13, 1979.![]() .'' Bull. London Math. Soc. 11, 268-272, 1979.
.'' Bull. London Math. Soc. 11, 268-272, 1979.![]() .'' Amer. Math. Monthly 97, 219-220, 1990.
.'' Amer. Math. Monthly 97, 219-220, 1990.![]() .'' Math. Intel. 1, 196-203, 1979.
.'' Math. Intel. 1, 196-203, 1979.