| 释义 |
Elliptic CurveInformally, an elliptic curve is a type of Cubic Curve whose solutions are confined to a region of space which istopologically equivalent to a Torus. Formally, an elliptic curve over a Field  is a nonsingular CubicCurve in two variables, is a nonsingular CubicCurve in two variables,  , with a , with a  -rational point (which may be a point at infinity). The Field -rational point (which may be a point at infinity). The Field  isusually taken to be the Complex Numbers isusually taken to be the Complex Numbers 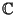 , Reals , Reals  ,Rationals ,Rationals 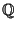 , algebraic extensions of , algebraic extensions of 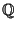 , p-adic Number , p-adic Number , or a Finite Field. , or a Finite Field.
By an appropriate change of variables, a general elliptic curve over a Field of Characteristic 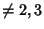
 | (1) |
 , ,  , ..., are elements of , ..., are elements of  , can be written in the form , can be written in the form
 | (2) |
 has Characteristic three,then the best that can be done is to transform the curve into has Characteristic three,then the best that can be done is to transform the curve into
 | (3) |
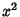 term cannot be eliminated). If term cannot be eliminated). If  has Characteristic two, then thesituation is even worse. A general form into which an elliptic curve over any has Characteristic two, then thesituation is even worse. A general form into which an elliptic curve over any  can be transformed is called theWeierstraß Form, and is given by can be transformed is called theWeierstraß Form, and is given by
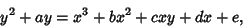 | (4) |
 , , 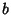 , , 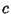 , ,  , and , and 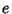 are elements of are elements of  .Luckily, .Luckily, 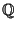 , ,  , and , and 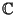 all have Characteristic zero. all have Characteristic zero.
Whereas Conic Sections can be parameterized by the rational functions, elliptic curves cannot. The simplest parameterization functions are Elliptic Functions. AbelianVarieties can be viewed as generalizations of elliptic curves.
If the underlying Field of an elliptic curve is algebraically closed, then a straight line cuts an elliptic curveat three points (counting multiple roots at points of tangency). If two are known, it is possible to compute the third.If two of the intersection points are  -Rational, then so is the third. Let -Rational, then so is the third. Let 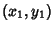 and and  be two points on an elliptic curve be two points on an elliptic curve 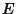 with Discriminant with Discriminant
 | (5) |
 | (6) |
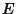 is defined as is defined as
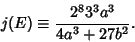 | (7) |
 | (8) |
For elliptic curves over 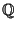 , Mordell proved that there are a finite number of integral solutions. TheMordell-Weil Theorem says that the Group of Rational Points of an elliptic curveover , Mordell proved that there are a finite number of integral solutions. TheMordell-Weil Theorem says that the Group of Rational Points of an elliptic curveover 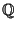 is finitely generated. Let the Roots of is finitely generated. Let the Roots of 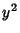 be be  , , 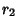 , and , and  . The discriminantis then . The discriminantis then
 | (11) |
The amazing Taniyama-Shimura Conjecture states that all rational elliptic curves are also modular. This fact is farfrom obvious, and despite the fact that the conjecture was proposed in 1955, it was not even partially proved until 1995. Even so, Wiles' proof of the semistable case surprised most mathematicians, who had believed the conjecture unassailable. As a side benefit, Wiles' proof of the Taniyama-Shimura Conjecture also laid to rest the famous and thorny problemwhich had baffled mathematicians for hundreds of years, Fermat's Last Theorem.
Curves with small Conductors are listed in Swinnerton-Dyer (1975) and Cremona (1997). Methods for computing integralpoints (points with integral coordinates) are given in Gebel et al. and Stroeker and Tzanakis (1994). See also Elliptic Curve Group Law, Fermat's Last Theorem, Frey Curve, j-Invariant, MinimalDiscriminant, Mordell-Weil Theorem, Ochoa Curve, Ribet's Theorem, Siegel's Theorem,Swinnerton-Dyer Conjecture, Taniyama-Shimura Conjecture, Weierstraß Form
References
 Elliptic Curves Elliptic CurvesAtkin, A. O. L. and Morain, F. ``Elliptic Curves and Primality Proving.'' Math. Comput. 61, 29-68, 1993. Cassels, J. W. S. Lectures on Elliptic Curves. New York: Cambridge University Press, 1991. Cremona, J. E. Algorithms for Modular Elliptic Curves, 2nd ed. Cambridge, England: Cambridge University Press, 1997. Cremona, J. E. ``Elliptic Curve Data.'' ftp://euclid.ex.ac.uk/pub/cremona/data/. Du Val, P. Elliptic Functions and Elliptic Curves. Cambridge: Cambridge University Press, 1973. Gebel, J.; Pethö, A.; and Zimmer, H. G. ``Computing Integral Points on Elliptic Curves.'' Acta Arith. 68, 171-192, 1994. Ireland, K. and Rosen, M. ``Elliptic Curves.'' Ch. 18 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 297-318, 1990. Katz, N. M. and Mazur, B. Arithmetic Moduli of Elliptic Curves. Princeton, NJ: Princeton University Press, 1985. Knapp, A. W. Elliptic Curves. Princeton, NJ: Princeton University Press, 1992. Koblitz, N. Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993. Lang, S. Elliptic Curves: Diophantine Analysis. Berlin: Springer-Verlag, 1978. Silverman, J. H. The Arithmetic of Elliptic Curves. New York: Springer-Verlag, 1986. Silverman, J. H. The Arithmetic of Elliptic Curves II. New York: Springer-Verlag, 1994. Silverman, J. H. and Tate, J. T. Rational Points on Elliptic Curves. New York: Springer-Verlag, 1992. Stroeker, R. J. and Tzanakis, N. ``Solving Elliptic Diophantine Equations by Estimating Linear Forms in Elliptic Logarithms.'' Acta Arith. 67, 177-196, 1994. Swinnerton-Dyer, H. P. F. ``Correction to: `On 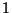 -adic Representations and Congruences for Coefficients of Modular Forms.''' In Modular Functions of One Variable, Vol. 4, Proc. Internat. Summer School for Theoret. Phys., Univ. Antwerp, Antwerp, RUCA, July-Aug. 1972. Berlin: Springer-Verlag, 1975. -adic Representations and Congruences for Coefficients of Modular Forms.''' In Modular Functions of One Variable, Vol. 4, Proc. Internat. Summer School for Theoret. Phys., Univ. Antwerp, Antwerp, RUCA, July-Aug. 1972. Berlin: Springer-Verlag, 1975.
|
![]() is a nonsingular CubicCurve in two variables,
is a nonsingular CubicCurve in two variables, ![]() , with a
, with a ![]() -rational point (which may be a point at infinity). The Field
-rational point (which may be a point at infinity). The Field ![]() isusually taken to be the Complex Numbers
isusually taken to be the Complex Numbers ![]() , Reals
, Reals ![]() ,Rationals
,Rationals ![]() , algebraic extensions of
, algebraic extensions of ![]() , p-adic Number
, p-adic Number![]() , or a Finite Field.
, or a Finite Field.![]()

![]() -Rational, then so is the third. Let
-Rational, then so is the third. Let ![]() and
and ![]() be two points on an elliptic curve
be two points on an elliptic curve ![]() with Discriminant
with Discriminant 
![]() Elliptic Curves
Elliptic Curves![]() -adic Representations and Congruences for Coefficients of Modular Forms.''' In Modular Functions of One Variable, Vol. 4, Proc. Internat. Summer School for Theoret. Phys., Univ. Antwerp, Antwerp, RUCA, July-Aug. 1972. Berlin: Springer-Verlag, 1975.
-adic Representations and Congruences for Coefficients of Modular Forms.''' In Modular Functions of One Variable, Vol. 4, Proc. Internat. Summer School for Theoret. Phys., Univ. Antwerp, Antwerp, RUCA, July-Aug. 1972. Berlin: Springer-Verlag, 1975.