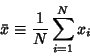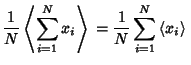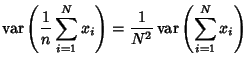| 释义 |
Arithmetic MeanFor a Continuous Distribution function, the arithmetic mean of the population, denoted 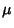 , ,  , , 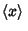 , or , or , is given by , is given by
 | (1) |
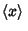 is the Expectation Value. For a Discrete Distribution, is the Expectation Value. For a Discrete Distribution,
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 and and  are Independent Statistics. The ``sample mean,'' which is the mean estimated from a statisticalsample, is an Unbiased Estimator for the population mean. are Independent Statistics. The ``sample mean,'' which is the mean estimated from a statisticalsample, is an Unbiased Estimator for the population mean.
For small samples, the mean is more efficient than the Median and approximately  less (Kenney and Keeping 1962, p. 211). A general expression which often holds approximately is less (Kenney and Keeping 1962, p. 211). A general expression which often holds approximately is
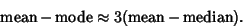 | (6) |
Given a set of samples  , the arithmetic mean is , the arithmetic mean is
 | (7) |
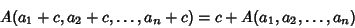 | (8) |
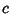 . The arithmetic mean satisfies . The arithmetic mean satisfies
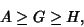 | (9) |
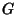 is the Geometric Mean and is the Geometric Mean and 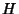 is the Harmonic Mean (Hardy et al. 1952; Mitrinovic 1970; Beckenbach andBellman 1983; Bullen et al. 1988; Mitrinovic et al. 1993; Alzer 1996). This can be shown as follows. For is the Harmonic Mean (Hardy et al. 1952; Mitrinovic 1970; Beckenbach andBellman 1983; Bullen et al. 1988; Mitrinovic et al. 1993; Alzer 1996). This can be shown as follows. For  , ,
 | (10) |
 | (11) |
 | (12) |
 | (13) |
 | (14) |
 . To show the second part of the inequality, . To show the second part of the inequality,
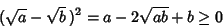 | (15) |
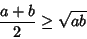 | (16) |
 | (17) |
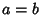 . Combining (14) and (17) then gives (9). . Combining (14) and (17) then gives (9).
Given 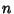 independent random Gaussian Distributed variates independent random Gaussian Distributed variates  , each with populationmean , each with populationmean  and Variance and Variance 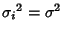 , ,
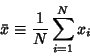 | (18) |
so the sample mean is an Unbiased Estimator of population mean. However, the distribution of  depends on the sample size. For large samples, depends on the sample size. For large samples,  is approximately Normal. For small samples, Student's t-Distribution should be used. is approximately Normal. For small samples, Student's t-Distribution should be used.
The Variance of the sample mean is independent of the distribution.
From k-Statistic for a Gaussian Distribution, the Unbiased Estimator forthe Variance is given by
 | (21) |
 | (22) |
 | (23) |
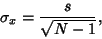 | (24) |
 | (25) |
 | (26) |
ReferencesAbramowitz, M. and Stegun, C. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 10, 1972.Alzer, H. ``A Proof of the Arithmetic Mean-Geometric Mean Inequality.'' Amer. Math. Monthly 103, 585, 1996. Beckenbach, E. F. and Bellman, R. Inequalities. New York: Springer-Verlag, 1983. Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 471, 1987. Bullen, P. S.; Mitrinovic, D. S.; and Vasic, P. M. Means & Their Inequalities. Dordrecht, Netherlands: Reidel, 1988. Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities. Cambridge, England: Cambridge University Press, 1952. Hoehn, L. and Niven, I. ``Averages on the Move.'' Math. Mag. 58, 151-156, 1985. Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962. Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M. Classical and New Inequalities in Analysis. Dordrecht, Netherlands: Kluwer, 1993. Vasic, P. M. and Mitrinovic, D. S. Analytic Inequalities. New York: Springer-Verlag, 1970. |
![]() ,
, ![]() ,
, ![]() , or
, or![]() , is given by
, is given by
![]() less (Kenney and Keeping 1962, p. 211). A general expression which often holds approximately is
less (Kenney and Keeping 1962, p. 211). A general expression which often holds approximately is![]() , the arithmetic mean is
, the arithmetic mean is
![]() independent random Gaussian Distributed variates
independent random Gaussian Distributed variates ![]() , each with populationmean
, each with populationmean ![]() and Variance
and Variance ![]() ,
,